Algèbres et sigma-algèbres
17 messages
- Page 1 sur 1
algèbres et sigma-algèbres
Bonjour, voici des exercices de théorie de la mesure, sur les sigma-algèbres. Pouvez-vous, s'il vous plaît, m'aider à les résoudre (même si ce n'est qu'une partie d'entre eux)?
1_ vérifier que l'union de deux sigma-algèbres n'est pas forcément une sigma-algèbre. Donner un exemple dans lequel les sigma-algèbres de partitions ont un nombre infinis d'éléments.
2_ Soit M une sigma-algèbre de cardinal infini. Démontrer que qu'elle a un cardinal non numérable.
3_ Soit delta une partition de N. Démontrer que delta est numérable.
Soit Mdelta={E inclus dans N tels que E est union d'éléments de delta}. Démontrer que Mdelta est une sigma-algèbre.
Démontrer que toute sigma-algèbre de N est de la forme Mdelta pour chaque partition de delta.
Merci d'avance pour votre aide!
1_ vérifier que l'union de deux sigma-algèbres n'est pas forcément une sigma-algèbre. Donner un exemple dans lequel les sigma-algèbres de partitions ont un nombre infinis d'éléments.
2_ Soit M une sigma-algèbre de cardinal infini. Démontrer que qu'elle a un cardinal non numérable.
3_ Soit delta une partition de N. Démontrer que delta est numérable.
Soit Mdelta={E inclus dans N tels que E est union d'éléments de delta}. Démontrer que Mdelta est une sigma-algèbre.
Démontrer que toute sigma-algèbre de N est de la forme Mdelta pour chaque partition de delta.
Merci d'avance pour votre aide!
1)
Pas facile de trouver un exemple simple avec des ensembles infinis !!
Un essai :
T1 = { A \in P(IR), A ou IR\A est dénombrable }
T2 = { A \in P(IR), tel que si 2n \in A alors 2n+1 \in A avec n entier }
ce sont deux sigma-algèbres
Alors
- A = 3Z \in T1
- B = U_n ]2n-1/4;2n+1/4[ U ]2n+1-1/4;2n+1+1/4[
R \ (AUB) n'est pas dans T1 U T2
3) a) le premier point est clair : il suffit de prendre un élément dans chaque ensemble formant la partition.
b) suffit de vérifier c'est simple
c) je pense qu'il suffit de considérer la relation d'équivalence (et la partition qui va avec) : x R y si y est dans le plus petit élément de la sigma-algèbre qui contient x.
Pas facile de trouver un exemple simple avec des ensembles infinis !!
Un essai :
T1 = { A \in P(IR), A ou IR\A est dénombrable }
T2 = { A \in P(IR), tel que si 2n \in A alors 2n+1 \in A avec n entier }
ce sont deux sigma-algèbres
Alors
- A = 3Z \in T1
- B = U_n ]2n-1/4;2n+1/4[ U ]2n+1-1/4;2n+1+1/4[
R \ (AUB) n'est pas dans T1 U T2
3) a) le premier point est clair : il suffit de prendre un élément dans chaque ensemble formant la partition.
b) suffit de vérifier c'est simple
c) je pense qu'il suffit de considérer la relation d'équivalence (et la partition qui va avec) : x R y si y est dans le plus petit élément de la sigma-algèbre qui contient x.
Pour le 2), il suffit de montrer que si la tribu est dénombrable elle est définie sur un ensemble dénombrable et contradiction.
On définit C(x) comme l'intersection de tous les éléments de la tribu contenant x, c'est lui aussi un élément de la tribu (bicoze tribu dénombrable)
On définit la relation d'équivalence (à vérifier mais facile) : x R y ssi x et y A(x).
Maintenant on prend la tribu engendrée par les A(x). Elle est contenue dans la tribu d'origine donc au plus dénombrable. Mais une tribu engendrée par une partition non finie ne peut pas être dénombrable.
On définit C(x) comme l'intersection de tous les éléments de la tribu contenant x, c'est lui aussi un élément de la tribu (bicoze tribu dénombrable)
On définit la relation d'équivalence (à vérifier mais facile) : x R y ssi x et y A(x).
Maintenant on prend la tribu engendrée par les A(x). Elle est contenue dans la tribu d'origine donc au plus dénombrable. Mais une tribu engendrée par une partition non finie ne peut pas être dénombrable.
Bonjour, tout d'abord, merci pour votre réponse. J'aimerais avoir plus de précisions:
_ Pour l'exercice 1, dans votre exemple, je ne suis pas sûre de comprendre les notations: 3Z représente les multiples de 3? Dans ce cas, que représent A union B?
_ Pour l'exercice 2, que représente A(x) dans la relation d'équivalence (et d'ailleurs pourquoi une relation d'équivalence?)? Et que veut dire «*au plus*» *dénombrable* (soit dit en passant, je m'excuse de dire numérable pour dénombrable, étant étudiant erasmus, j'en perds mon français/math!!)? Enfin, pourquoi «*une tribu engendrée par une partition non finie ne peut pas être dénombrable*»? Bref, pouvez-vous s'il vous plaît, plus détailler et expliquer.
_ Pour l'exercice 3, je n'arrive pas à vérifier que le complémentaire d'un élément de Mdelta est dans Mdelta. En effet, le complémentaire de l'union d'éléments de delta est l'intersection des complémentaires; de là, je voudrais que cela soit égal à une union d'éléments de delta pour qu'il soit dans Mdelta.
Pouvez-vous également détailler la troisième partie de l'exercice 3?
Encore merci et à bientôt.
_ Pour l'exercice 1, dans votre exemple, je ne suis pas sûre de comprendre les notations: 3Z représente les multiples de 3? Dans ce cas, que représent A union B?
_ Pour l'exercice 2, que représente A(x) dans la relation d'équivalence (et d'ailleurs pourquoi une relation d'équivalence?)? Et que veut dire «*au plus*» *dénombrable* (soit dit en passant, je m'excuse de dire numérable pour dénombrable, étant étudiant erasmus, j'en perds mon français/math!!)? Enfin, pourquoi «*une tribu engendrée par une partition non finie ne peut pas être dénombrable*»? Bref, pouvez-vous s'il vous plaît, plus détailler et expliquer.
_ Pour l'exercice 3, je n'arrive pas à vérifier que le complémentaire d'un élément de Mdelta est dans Mdelta. En effet, le complémentaire de l'union d'éléments de delta est l'intersection des complémentaires; de là, je voudrais que cela soit égal à une union d'éléments de delta pour qu'il soit dans Mdelta.
Pouvez-vous également détailler la troisième partie de l'exercice 3?
Encore merci et à bientôt.
ThSQ a écrit:sauf si une bonne âme s'est pas dévouée d'ici là ...).
N y a t il pas qque chose de contradictoire la?XD
Sinon,je suis pas trop une bonne ame,ce soir...Je dirai juste que si Delta est en bijection avec N,Mdelta ressemble fortement a P(N).Et aussi que pour la 1 ya je pense plus simple en utilisant des Mdelta justement.Par exemple prendre Delta1 la partition des {2k,2k+1} et Delta2 la partition des {3k,3k+1,3k+2}...(remarquer que {2} est l intersection de {0,1,2} et {2,3})
Bonjour, pour la réponse de ffpower dans l'exercice 1, peut-elle être détaillée? En quoi l'union de delta1 et delta2 n'est-elle pas une sigma-algèbre? L'idée serait de dire que {2} n'est pas présent dans les deux sigma-algèbre mais dans l'union? Pourtant il est considèré comme intersection.
Dans la remarque pour l'exercice 3 "Je dirai juste que si Delta est en bijection avec N,Mdelta ressemble fortement a P(N)", Mdelta est une union d'éléments de delta, tandis qu'une partition de N est une union disjointe, non?
J'espère toujours les réponses à mes autres questions :+)!
Encore merci en tout cas!
Dans la remarque pour l'exercice 3 "Je dirai juste que si Delta est en bijection avec N,Mdelta ressemble fortement a P(N)", Mdelta est une union d'éléments de delta, tandis qu'une partition de N est une union disjointe, non?
J'espère toujours les réponses à mes autres questions :+)!
Encore merci en tout cas!
Tu en es où Anamath ?
Je te fais celui-là car c'est le plus joli je trouve :happy2:
On prend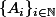 une partition dénombrable engendrant une tribu T sur E.
une partition dénombrable engendrant une tribu T sur E.
Soit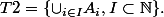
C'est clair que T doit contenir T2. C'est clair aussi que T2 est une tribu (seul le passage au complémentaire est délicat mais :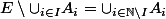 )
)
C'est clair aussi que T2 est de taille > \mathbb{N})
( c'est clair non ? )
Je te fais celui-là car c'est le plus joli je trouve :happy2:
Une tribu engendrée par une partition non finie ne peut pas être dénombrable
On prend
Soit
C'est clair que T doit contenir T2. C'est clair aussi que T2 est une tribu (seul le passage au complémentaire est délicat mais :
C'est clair aussi que T2 est de taille
( c'est clair non ? )
Bonjour,
désolée, j'en perds le fil, ce que vous venez de démontrer correspond à quelle partie de quel exercie?
Voici où j'en suis: j'ai terminé l'exercice 1, le 2 est plus ou moins fini mais le trois ne l'est pas; surtout pour «*démontrer que toute sigma algèbre de N est de la forme Mdelta (comme dans la citation de l'exo)*». Je n'arrive pas non plus à vérifier la stabilité par passage au complémentaire pour Mdelta.
désolée, j'en perds le fil, ce que vous venez de démontrer correspond à quelle partie de quel exercie?
Voici où j'en suis: j'ai terminé l'exercice 1, le 2 est plus ou moins fini mais le trois ne l'est pas; surtout pour «*démontrer que toute sigma algèbre de N est de la forme Mdelta (comme dans la citation de l'exo)*». Je n'arrive pas non plus à vérifier la stabilité par passage au complémentaire pour Mdelta.
Bonjour, il suffit de ne pas écrire du week-end pour se retrouver très loin dans la liste! :we: !
Pouvez-vous, s'il vous plaît, m'aider sur les deux derniers points que j'ai cité dans ma dernière réponse?
Egalement, si vous pouviez m'aider pour les exercices suivant:
Soit (X1, M1, u1) un espace de mesure complet.
Soit g: X1 --> X2 un application, M2={A inclus dans X2:g-1(A) appartient à M1}, u2=u1(g-1(A)). Prouver que (X2, M2, u2) est un espace de mesure complet.
J'ai déjà montré que M2 était une sigma-algèbre, que u2 était une mesure. En ce qui concerne l'espace complet, voici ce à quoi j'ai pensé, donnez-moi s'il vous plaît votre avis:
J'ai considéré le sous-ensemble des ensembles mesurables de mesure nulle:
N' ={S inclus dans X2: il existe N dans M2-u2° avec S inclus dans N}. Je dois donc prouver que N' est inclus dans M2.
«*il existe N dans M2-u2°*» signifie u2(N)=0
signifie u1(g-1(N))=0
Signifie g-1(N) dans M1u1°
Comme (X1,M1,u1) complet: cela signifie N' dans M2.
Voici l'autre exercice:
démontrer qu'un algèbre A dans X est une sigma algèbre si et seulement si «*si Ei appartient à A, et E1 inclus dans E2 inclus dans, ... , alors l'union infinie des Ei est dans A.*»
Ce que je ne comprends pas c'est que pour moi, on définie une sigma algèbre justement en précisant que c'est une algèbre qui a cette dernière propriété. Alors comment faire une démonstration?
Merci et à bientôt!
PS:Je suis en Espagne!
Pouvez-vous, s'il vous plaît, m'aider sur les deux derniers points que j'ai cité dans ma dernière réponse?
Egalement, si vous pouviez m'aider pour les exercices suivant:
Soit (X1, M1, u1) un espace de mesure complet.
Soit g: X1 --> X2 un application, M2={A inclus dans X2:g-1(A) appartient à M1}, u2=u1(g-1(A)). Prouver que (X2, M2, u2) est un espace de mesure complet.
J'ai déjà montré que M2 était une sigma-algèbre, que u2 était une mesure. En ce qui concerne l'espace complet, voici ce à quoi j'ai pensé, donnez-moi s'il vous plaît votre avis:
J'ai considéré le sous-ensemble des ensembles mesurables de mesure nulle:
N' ={S inclus dans X2: il existe N dans M2-u2° avec S inclus dans N}. Je dois donc prouver que N' est inclus dans M2.
«*il existe N dans M2-u2°*» signifie u2(N)=0
signifie u1(g-1(N))=0
Signifie g-1(N) dans M1u1°
Comme (X1,M1,u1) complet: cela signifie N' dans M2.
Voici l'autre exercice:
démontrer qu'un algèbre A dans X est une sigma algèbre si et seulement si «*si Ei appartient à A, et E1 inclus dans E2 inclus dans, ... , alors l'union infinie des Ei est dans A.*»
Ce que je ne comprends pas c'est que pour moi, on définie une sigma algèbre justement en précisant que c'est une algèbre qui a cette dernière propriété. Alors comment faire une démonstration?
Merci et à bientôt!
PS:Je suis en Espagne!
Anamath a écrit:c'est une algèbre qui a cette dernière propriété. Alors comment faire une démonstration?
Je crois pas ici il est question d'une union d'ensembles "croissants" et pas d'ensembles quelconques.
Ceci dit passer de l'un à l'autre c'est pas dur.
La suite
Tu es en Espagne ? En colloc avec une anglaise, une belge, un allemand et un italien ?
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
