Récurrence amusante
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
 par Alpha » 02 Oct 2005, 12:43
par Alpha » 02 Oct 2005, 12:43
Bonjour à tous,
Je vous soumets cette amusante "démonstration" de la propriété suivante :
Soit

. Alors pour tout
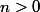
, on a

.
"En effet", c'est vrai pour

, et, supposant que c'est vrai pour
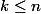
,
on conclut car :
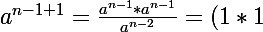/1=1)
Cherchez l'erreur... :happy3:
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 02 Oct 2005, 13:21
par rene38 » 02 Oct 2005, 13:21
Salut
L'hérédité faisant intervenir les indices (qui, dans le cas présent, sont des exposants) n-1 ET n-2, l'initialisation doit se faire pour n=1 ET n=2 et là ... ça coince.
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
 par Alpha » 02 Oct 2005, 16:57
par Alpha » 02 Oct 2005, 16:57
Oui, rene38, je suis tout à fait d'accord!
C'est un exemple qui insiste, en tout cas, sur l'importance de bien vérifier son initialisation lors d'une récurrence!
Cordialement :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités