Les ensembles

Bonsoir,

j'aimerais comprendre la difference entre le complementaire et la difference

difference: A\B = {x € A | x appartient pas B}
complementaire de A dans B = { x € B | x appartient pas A}

Moi je pense que la reponse est que les deux operations sont inverse.

Merci.

Rain' a écrit:Pour le complémentaire , A est une partie de B.

Pour la différence A et B sont quelconques. A\B = {x | x €A et x n'app pas à B}

Ben d'apres la definition qu'a donné le prof

difference: A\B = {x € A | x appartient pas B}
complementaire de A dans B = { x € B | x appartient pas A}

A n'est pas une partie de B (voir image sur ce lien http://www.maths-express.com/bac-exo/bac-s/cour-s/cours-proba/complementaire.htm ), ton cas est un cas particulier.

Rain' a écrit:C'est pas ce qu'en dit wiki, mais bon wiki a parfois (souvent ?) tort

lol :ptdr:

selon m'a definitu=ion (enfin celle donnée par le prof) penses tu que ce sont 2 relation inverse ...

il y a trois quart de siècle que je n'ai pas actualisé ma définition de complémentaire

mais complémentaire de A dans B indique clairement que A est une partie de B

T'as quel age "fahr451" ? :lol2:

fahr451 a écrit:il y a trois quart de siècle que je n'ai pas actualisé ma définition de complémentaire

mais complémentaire de A dans B indique clairement que A est une partie de B

ben d'apres la definition du prof et celle que j'ai pus trouver sur de nombreux site internet, je peux te dire que non, A n'est pas forcement une partie de B, à moins que je comprenne mal la definition de "PARTIE" .

Il y a bien rapprochement entre complémentaire et différence. Il y a deux mots parcequ'on les utilise dans des cadres différents (parfois le complémentaire apparaît plus naturel, parfois c'est la différence, bien que si on peut définir quelquechose avec l'un, on peut le faire avec l'autre).

Le complémentaire d'un ensemble A dans un autre ensemble B, c'est l'ensemble des points qui appartiennent à B et pas à A (l'opposé dans B).
La différence de A par B A\B c'est l'ensemble A dont on vire tout ce qui n'appartient pas à B. Du coup, on a bien A\B = complémentaire de A dans B.
A\B = A

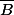
Quelle différence alors? et bien, généralement on parle du complémentaire d'un ensemble dans l'ensemble dans lequel on travaille (souvent c'est E. pour le complémentaire de A dans B, on prends A inclus dans B (bien que la définition du complémentaire soit effectivement plus générale... mais c'est un peu débile : quels éléments de ta peau n'appartiennent pas à ton corps?...)), alors qu'on fait la différence de deux ensembles quelconques inclus dans l'ensemble de travail.

Exemples :
le complémentaire de [0;1] dans R est ]-;0[U]1;+ (= R\[0;1] )
la différence de [0;1] par [1/2;2] est [0;1[ (qui est aussi le complémentaire de [0;1] dans [0;1]U[1/2;2], ce qu'on ne dira presque jamais sauf pour embeter son monde)