Arithmétique : fermat
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 15 Juin 2007, 22:55
par prody-G » 15 Juin 2007, 22:55
salut à tous
voilà j'ai trouvé ce petit exo sur le net et j'ai l'impression qu'il y a un petit problème dans l'énoncé...

ça ne serait pas plutôt
=p(_{k-1}^{p-1}))
?
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juin 2007, 00:08
par aviateurpilot » 16 Juin 2007, 00:08
oui
prody-G **
}{\(_{k-1}^{p-1}\)}=\frac{p!(k-1)!(p-k)}{(p-1)!k!(p-k)!}=\frac{p}{k})
donc

et par suite:
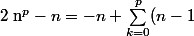^k \(_k^p\)\equiv -n+1+(n-1)^p\ (mod\ p)\equiv (n-2)^{p}-(n-2) \equiv...\equiv 0^p-0\(mod\ p)\equiv 0\(mod\ p))
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 16 Juin 2007, 11:52
par prody-G » 16 Juin 2007, 11:52
merci aviateurpilot
Pour la deuxième est-ce que tu pourrais me donner la démonstration de l'égalité que tu as utilisée
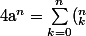(a-1)^n)
?
J'ai essayé de le faire par récurrence, sans réussite...
Mais elle est vraiment pas mal cette égalité, je connaissais pas. Bien vu !
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 16 Juin 2007, 12:23
par sue » 16 Juin 2007, 12:23
c'est le binome de Newton :
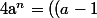+1)^n=\sum_{k=0}^n(_k^n)(a-1)^k)
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Juin 2007, 16:50
par fahr451 » 16 Juin 2007, 16:50
à noter que la relation se démontre sans l 'aide des factoriels et se retient aisément
considérer un ensemble de p personnes parmi lesquelles on choisit k individus pour faire une équipe de hand et parmi ceux là un gardien
suivant qu 'on choisit d 'abord l'équipe puis le gardien ou l'inverse on a la relation
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Juin 2007, 18:18
par yos » 16 Juin 2007, 18:18
fahr451 a écrit:considérer un ensemble de p personnes parmi lesquelles on choisit k individus pour faire une équipe de hand et parmi ceux là un gardien
suivant qu 'on choisit d 'abord l'équipe puis le gardien ou l'inverse on a la relation
On peut aussi choisir m gardiens parmi les k individus parce que
1) On a plus de chance de gagner le match.
2) On obtient une relation plus générale :
(_m^k)=(_m^p)(_{k-m}^{p-m}))
.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Juin 2007, 18:21
par fahr451 » 16 Juin 2007, 18:21
oui plus générale mais moins utile "en pratique " (pas pour acheter son pain on est d 'accord)
le cas important est 1 gardien ( loi binomiale, polynômes de bernstein , loi hypergéo) voire un gardien et un avant (mêmes exemples)
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 16 Juin 2007, 21:20
par prody-G » 16 Juin 2007, 21:20
merci à tous pour vos réponses. J'me disais y avait le binôme de newton quelquepart mais bon avec (a+0)^n on avance pas beaucoup...^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités

