Arithmétique (Fermat)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Julius
- Membre Naturel
- Messages: 29
- Enregistré le: 01 Nov 2006, 11:24
-
 par Julius » 26 Avr 2007, 12:23
par Julius » 26 Avr 2007, 12:23
Je cale sur un exo d'arithmétique...
Soit x un entier. Montrer en utilisant le petit théorème de Fermat que x^21

x [3] et que x^21

x [11].
En déduire que : x^21

x [33]
Merci d'avance :++:
-
RadarX
- Membre Relatif
- Messages: 333
- Enregistré le: 24 Juil 2005, 19:39
-
 par RadarX » 26 Avr 2007, 20:43
par RadarX » 26 Avr 2007, 20:43
Julius a écrit:Je cale sur un exo d'arithmétique...
Soit x un entier. Montrer en utilisant le petit théorème de Fermat que x^21

x [3] et que x^21

x [11].
En déduire que : x^21

x [33]
Merci d'avance :++:
Je pourrais y reflechir si tu rappelais un peu ce que dit ce thm.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Avr 2007, 21:00
par Nightmare » 26 Avr 2007, 21:00
Bonsoir
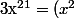^{10}\times x)
Or d'après le petit théorème de Fermat, comme 3 est premier :
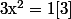
d'où :
^{10}\times x=1^{10}\times x=x[3])
:happy3:
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 26 Avr 2007, 21:05
par Clembou » 26 Avr 2007, 21:05
Nightmare a écrit:Bonsoir
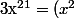^{10}\times x)
Or d'après le petit théorème de Fermat, comme 3 est premier :
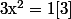
d'où :
^{10}\times x=1^{10}\times x=x[3])
:happy3:
attention nightmare, si tu veux obtenir le signe égal avec 3 barres en LaTeX : tapes [ tex ] \equiv [ /tex ]
-
RadarX
- Membre Relatif
- Messages: 333
- Enregistré le: 24 Juil 2005, 19:39
-
 par RadarX » 26 Avr 2007, 21:16
par RadarX » 26 Avr 2007, 21:16
Clembou a écrit:Ma politique :
J'aime aider les gens mais il faut que ça serve à quelque chose. Si vous ne comprenez pas une de mes explications, posez moi la question. Je déteste quand quelqu'un humilie un autre qui demande de l'aide. Un merci me suffit pour me récompenser de mon travail
Belle politique!! j'adhere! :++:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Avr 2007, 21:21
par Nightmare » 26 Avr 2007, 21:21
Je ne cherche pas à obtenir le signe = avec 3 barres Clembou :lol3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Avr 2007, 21:22
par Nightmare » 26 Avr 2007, 21:22
On a bien une égalité de classes d'équivalence, donc le égal est justifié.
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 26 Avr 2007, 21:24
par prody-G » 26 Avr 2007, 21:24
ah bon je pensais aussi que tu voulais avoir le symbole de congruences.
A priori x²=1[3] ça veut rien dire, non ? si ? lol
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 26 Avr 2007, 21:33
par Nightmare » 26 Avr 2007, 21:33
Si cela veut dire que x² est égal à 1 modulo 3.
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 26 Avr 2007, 21:38
par quinto » 26 Avr 2007, 21:38
On a vraiment l'égalité dans Z/2Z.
La notation [2] peut être interprétée comme +2Z.
Et puis ce n'est qu'une question de notation, pas de quoi en faire un plat, surtout si c'est juste.
-
Julius
- Membre Naturel
- Messages: 29
- Enregistré le: 01 Nov 2006, 11:24
-
 par Julius » 29 Avr 2007, 00:13
par Julius » 29 Avr 2007, 00:13
Merci de vos réponses^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
 x [3] et que x^21
x [3] et que x^21  x [11].
x [11]. x [33]
x [33] x [3] et que x^21
x [3] et que x^21  x [11].
x [11]. x [33]
x [33]