Spé math: nombres de fermat
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Kah
- Membre Rationnel
- Messages: 540
- Enregistré le: 15 Sep 2008, 19:51
-
 par Kah » 05 Oct 2008, 16:45
par Kah » 05 Oct 2008, 16:45
Bonjour, je coince sur cet exercice:
Soit Fn=

1) Montrer que si a divise b, alors

divise
 Fait, jusque la, sa va!
Fait, jusque la, sa va!2) Montrer que

>ou egal a n+1
fait aussi par recurrence sur n3) Montrer que Fn divise2^2^(n+1)-1
La, je coince, j'ai bien essayé d'ecrire Fn sous une forme comme x^a-1... Mais je n'y arrive pas.4) Montrer que Fn divise2^(Fn-1)-1
idem...Merci d'avance pour vos reponses.

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 05 Oct 2008, 16:58
par raito123 » 05 Oct 2008, 16:58
Salut,
On a une identité remarquable :
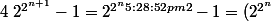^2-1 =(2^{2^n }+1)(2^{2^n }-1) = F_n\time(2^{2^n }-1))
Là tu dois conclure !!
Bonne chance pour la suite

Les multiples ne doivent pas être utilisés sans nécessité
-
Kah
- Membre Rationnel
- Messages: 540
- Enregistré le: 15 Sep 2008, 19:51
-
 par Kah » 05 Oct 2008, 17:01
par Kah » 05 Oct 2008, 17:01
raito123 a écrit:Salut,
On a une identité remarquable :
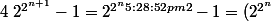^2-1 =(2^{2^n }+1)(2^{2^n }-1) = F_n\time(2^{2^n }-1))
Là tu dois conclure !!
Bonne chance pour la suite

Rah mais pourquoi j'y avais pas pensé! Merci beaucoup en tout cas. Pas d'idées pour la suite?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
