Geometrie dans l espace..

Bonjour, a tous et a toutes!

Jespere que vous m'aidez :) avec les reponses que je vais vous donnez


Voici l exos: On considere les points A (2 3 1 ) B ( 3 5 2) et C (0 3 2 )

A determiner le point L intersection de la droite (AB) avec le plan (xOy)
J ai fais: Etant sur un plan ( xOy) le point L a pour coordonnées ( x; y; O) ou z=0

Ensuite: Demontrer que les points A B C definnissent un plan.

J ai fais: Comme on n a deux vecteurs Non colineaires qui sont AB ( 1 2 1 ) et AC ( -2 0 1) Donc A B C ne definissent pas un plan.


A partir de la je suis bloquer :mur: :mur:

Ensuite a) soit le point N ( 2 Yn 4 ). Determiner les coordonnes de N pour que les points A B C et N soient coplanaires.

b) Soit a un reel determiner le point R ( a; a-1; 1-a) tel que AR et AB soient orthogonaux.

c) Soit D la droite passant par le point B de vecteurs directeur u( -2 3 -4 )
On considere un point M x y z ) du plan P passant par A et perpendiculaire a la droite D
Determiner les relations entre les coordonnees x y et z du point M.

Bonjour

Tout d'abord, peux-tu m'indiquer ton niveau : TS, je suppose?

A(2, 3, 1) ; (1, 2, 1) ; N(2, Yn, 4 )

Si un point se trouve sur la droite AB, il vérifie le système d'équations paramétriques suivant :
x = 2 + t
y = 3 +2t
z = 1 + t

Le plan (xOy) a pour équation z=0, donc L(xL, yL, 0)
0 = 1 + t, donc t = -1
En remplaçant t = -1 dans x et y on a xL et yL=1 L(1, 1, 0)

J ai fais: Comme on n a deux vecteurs Non colineaires qui sont AB ( 1 2 1 ) et AC ( -2 0 1) Donc A B C ne definissent pas un plan.

Rectification
les points A B C définissent un plan

Si les points A B C et N sont coplanaires :
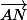= a + b

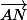(0, yn-3, 3)
a - 2b = 0
a + b = 3

a = 6 et b = 3 ; donc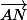 (0, 12, 3) et N( 2, 15, 4 )

La suite t'appartient...

Cordialement

Merci beaucoup.. pour la queston sur le plan je n avais pas bien lu la question.. je croyais qu il fallait demontrer qu il n y avait pas de plan defeni.. OupsSS
Je vais maintenant faire la suite et je vous en redirez des nouvelles.

Cordialement :we: