Démo concernant le sup !

Salut tout le monde
qui sait comment prouver mathématiquement la relation qui existe entre sup(A) sup(B) et sup(A inter B) ?
Merci !
Bon courage!

sandrine_guillerme a écrit:Salut tout le monde
qui sait comment prouver mathématiquement la relation qui existe entre sup(A) sup(B) et sup(A inter B) ?
Merci !
Bon courage!

C'est quoi A et B des intervalles de R ? des parties d'un ensemble quelconque ordonné ?

juste que sup(AB) X <= sup(A) et X <= sup(B) pour tout X de AB, donc en particulier pour sup(AB)

?

alben a écrit:C'est quoi A et B des intervalles de R ? des parties d'un ensemble quelconque ordonné ?

ba A et B sont deux parties d'un ensemble ordonné disons R par exemple ..et pis je souhaiterais une relation générale stp? merci!
Sa va nox ?

waip tranquillou et toi ?

Relation générale jcrois que dans le cas que tu donnes t'auras pas plus que ce que j'ai mis...Ou alors y'a un truc que je vois pas...

nox a écrit:juste que sup(AB) X <= sup(A) et X <= sup(B) pour tout X de AB, donc en particulier pour sup(AB)

?

Si tu pourrais m'éclaircir un peu plus encoe ça serait grandement apprècié!

à quel niveau ?

nox a écrit:juste que sup(AB) X <= sup(A) et X <= sup(B) pour tout X de AB, donc en particulier pour sup(AB)

?

On a l droit d'écrire la première équivalence? si Oui prouve le moi stp ?
(je parle de la première que tu as écris!)

ba si X est dans AB, X est dans A et X est dans B.
Donc X est inférieur au sup de A et au sup de B

hummOuais !
Et en termes d'inclusion?

euh...précise ta question...

Inclusion donc au niveau des ensembles ? à part AB inclus dans A et B je vois pas trop quoi dire de plus...

nan
plutot kant on remplace (inter) par (union)
Je me suis trompé je m'excuse

Si A et B sont deux intervalles de R, alors on a l'égalité.
sup(AB)=Inf(sup(A),sup(B))
Si l'un des ensemble est inclus dans l'autre, on a bien sur aussi l'égalité puisque l'intersection est l'ensemble inclus

alben a écrit:Si A et B sont deux intervalles de R, alors on a l'égalité.
sup(AB)=Inf(sup(A),sup(B))
Si l'un des ensemble est inclus dans l'autre, on a bien sur aussi l'égalité puisque l'intersection est l'ensemble inclus

Tout à fais d'accord avec toi maieuh .. J'ai mal enoncé ma question ! :mur:
Je récapitule je veux prouver mathématiquement une relation en tre sup(A union B ), sup(A) et sup(B)
Merci.

Pour l'union alors on a l'égalité.
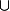
sup(AB)=Sup(sup(A),sup(B))
Le Sup est le plus petit des majorants.
Si M=Sup(A)>Sup(B), alors M est majorant de A et également de B, c'est le plus petit car s'il en existait un autre, inférieur, il serait majorant de A ce qui est impossible...

Ne pense tu que ça serais plus correcte d montrer la double inclusion pour montrer l'égalité?

sandrine_guillerme a écrit:Ne pense tu que ça serais plus correcte d montrer la double inclusion pour montrer l'égalité?

La double inclusion, c'est pour montrer l'égalité de deux ensembles, ici il s'agit de nombres :happy2:

ok merci bien

alben a écrit:Si A et B sont deux intervalles de R, alors on a l'égalité.
sup(AB)=Inf(sup(A),sup(B))
Si l'un des ensemble est inclus dans l'autre, on a bien sur aussi l'égalité puisque l'intersection est l'ensemble inclus

ah oui c'est vrai qu'on s'est mis dans un ensemble ordonné ^^