Question concernant les limites
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
quaresma
- Membre Relatif
- Messages: 294
- Enregistré le: 28 Juin 2005, 15:08
-
 par quaresma » 14 Avr 2008, 21:14
par quaresma » 14 Avr 2008, 21:14
Bonjour à tous,
lorsque j'ai une limite de ce genre qui tend vers + l'infini :
 = x^2 + 3x + 5)
Que dois-je faire de la constante ?
Sachant que x²=>

et 3x=>

Merci pour vos réponses :happy2:
-
Moutth
- Membre Naturel
- Messages: 59
- Enregistré le: 14 Avr 2008, 19:47
-
 par Moutth » 14 Avr 2008, 21:25
par Moutth » 14 Avr 2008, 21:25
salut
pour quelqu'un du supérieur un peu "limite" comme question... lol
ok je sors :marteau:
pour un polynome et en + infini tu prend la limite du terme du plus haut degré
-
quaresma
- Membre Relatif
- Messages: 294
- Enregistré le: 28 Juin 2005, 15:08
-
 par quaresma » 14 Avr 2008, 21:29
par quaresma » 14 Avr 2008, 21:29
A cause du 5 je suis obligé de mettre x² en facteur donc ?
-
Moutth
- Membre Naturel
- Messages: 59
- Enregistré le: 14 Avr 2008, 19:47
-
 par Moutth » 14 Avr 2008, 21:32
par Moutth » 14 Avr 2008, 21:32
tu m'as mal compris
la limite de ta fonction x^2+3x+5 est egale a la limite de x^2
autrement dit +infini
-
quaresma
- Membre Relatif
- Messages: 294
- Enregistré le: 28 Juin 2005, 15:08
-
 par quaresma » 14 Avr 2008, 21:39
par quaresma » 14 Avr 2008, 21:39
En BTS, ils nous demande tjs de démontrer, voici mon cheminement :
)
)
)
Arrivée à
)
Le "1" me dérange, je ne sais pas quoi en faire... :briques:
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 14 Avr 2008, 21:41
par Babe » 14 Avr 2008, 21:41
"1 x oo = oo "
-
quaresma
- Membre Relatif
- Messages: 294
- Enregistré le: 28 Juin 2005, 15:08
-
 par quaresma » 14 Avr 2008, 21:43
par quaresma » 14 Avr 2008, 21:43
Babe a écrit:"1 x oo = oo "
En effet quel *** !!
grazie
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 14 Avr 2008, 22:00
par Joker62 » 14 Avr 2008, 22:00
ça choque beaucoup de monde que lim (x->+oo) 5 = 5
Et en n'oubliant pas que +oo + 5 = +oo, on peut conclure
-
quaresma
- Membre Relatif
- Messages: 294
- Enregistré le: 28 Juin 2005, 15:08
-
 par quaresma » 14 Avr 2008, 22:08
par quaresma » 14 Avr 2008, 22:08
Joker62 a écrit:ça choque beaucoup de monde que lim (x->+oo) 5 = 5
Why ? :id:
-
Moutth
- Membre Naturel
- Messages: 59
- Enregistré le: 14 Avr 2008, 19:47
-
 par Moutth » 14 Avr 2008, 22:26
par Moutth » 14 Avr 2008, 22:26
5 ne dépendant pas de x (c'est une constante) sa limite ne varie pas et est égale a lui meme cad 5
-
quaresma
- Membre Relatif
- Messages: 294
- Enregistré le: 28 Juin 2005, 15:08
-
 par quaresma » 04 Mai 2008, 22:00
par quaresma » 04 Mai 2008, 22:00
Juste une question,
pourquoi le resultat de cette limite est +l'infini?
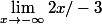
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 04 Mai 2008, 23:51
par Joker62 » 04 Mai 2008, 23:51
Le numérateur tend vers +oo
Le dénominateur est négatif
Un très grand nombre divisé par un négatif donne un très petit nombre
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 05 Mai 2008, 01:54
par MacManus » 05 Mai 2008, 01:54
le numérateur tend vers 2*(-infini) = -infini ('',)
-
quaresma
- Membre Relatif
- Messages: 294
- Enregistré le: 28 Juin 2005, 15:08
-
 par quaresma » 05 Mai 2008, 02:55
par quaresma » 05 Mai 2008, 02:55
MacManus a écrit:le numérateur tend vers 2*(-infini) = -infini ('',)
oui c bien ce que je me disais.
On peut donc considérer la chose suivante:

=

=

=

non?
-
quaresma
- Membre Relatif
- Messages: 294
- Enregistré le: 28 Juin 2005, 15:08
-
 par quaresma » 05 Mai 2008, 08:30
par quaresma » 05 Mai 2008, 08:30
Mais ma réponse pourrait convenir aussi non ?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 05 Mai 2008, 15:11
par Joker62 » 05 Mai 2008, 15:11
en plus j'ai lu bizarrement la limite en +oo
Faut j'fasse attention moi :^)
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 05 Mai 2008, 16:39
par emdro » 05 Mai 2008, 16:39
Bonjour,
Plusieurs choses à la limite de l'erreur dans ces écritures...
Je ne vois pas comment vous pouvez écrire

,
Eventuellement
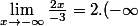 \times \frac{1}{-3}<br /><br />= - \infty \times \frac{1}{-3}<br /><br />= + \infty)
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 05 Mai 2008, 16:40
par emdro » 05 Mai 2008, 16:40
Quant à
<br /><br />=\lim_{x \to + \infty} x^2(1+0+0))
,
vous êtes mal partis si vous vous permettez de prendre ce genre de liberté...
-
quaresma
- Membre Relatif
- Messages: 294
- Enregistré le: 28 Juin 2005, 15:08
-
 par quaresma » 05 Mai 2008, 19:52
par quaresma » 05 Mai 2008, 19:52
emdro a écrit:Eventuellement
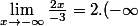 \times \frac{1}{-3}<br /><br />= - \infty \times \frac{1}{-3}<br /><br />= + \infty)
lut emdro,
oui c'est ce que je voulais ecrire.
emdro a écrit:Quant à
<br /><br />=\lim_{x \to + \infty} x^2(1+0+0))
,
vous êtes mal partis si vous vous permettez de prendre ce genre de liberté...
Et comment vois-tu la formulation ?
merci pour ton aide
@+ D@ms
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités