Méthode concernant les intégrales généralisées.

[Pederle]

Bonsoir,

Soit g la fonction définie par g(x)=int((a^x)/(1+a))da, avec l'intégrale entre 0 et +infini (désolé j'arrive pas a l'écrire en language "matheux" :$)

Quelle est la méthode pour trouver les valeurs de x pour que la fonction g(x) existe? Merci.

[abcd22]

Bonsoir,
Il faut étudier l'intégrabilité de la en 0 et en + infini en fonction de x.

[buuuu]

Je pense déjà que a doit etre strictement positif,

car a^x= exp ( x log a)

a suivre...

[Pythales]

est entre et !

[Pythales]

Pour on doit avoir
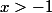
Pour on doit avoir
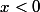
En résumé

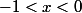
[buuuu]

oui pardon, j'ai pas remarqué qu'on integrait par rapport au a,

mais pardon, je vois pas comment vous avez trouver les valeurs de x, sur qeuls criteres vous vous etes basés?!