Prouver qu'un point appartient à une doite
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Frednight
- Membre Rationnel
- Messages: 616
- Enregistré le: 04 Fév 2007, 17:03
-
 par Frednight » 11 Sep 2014, 18:26
par Frednight » 11 Sep 2014, 18:26
Bonsoir à tous
Je rencontre un problème :
Soient trois points
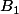
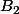
et
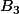
tels que
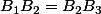
, et trois autres points


et
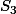
tels que

On note

(resp.
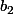
et
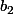
) la droite
)
(resp.
)
et
)
).
On trace la droite
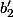
(resp.
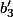
) la droite parallèle à
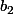
(resp.
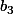
) et passant par

On trace une droite perpendiculaire à

en point qu'on nomme

. Cette droite coupe
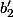
en un point que l'on nomme

.
On nomme

le point symétrique à

par

. La droite parallèle à

et passant par

coupe
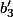
en un point

.
La droite
)
coupe

en un point

.
On trace la parallèle à
)
passant par

Je souhaiterais démontrer que la translation du point

par le vecteur
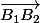
appartient à cette dernière droite
)
mais je n'y parviens pas.
Je suppose que cela est en partie explicable par l'égalité

mais sans arriver à progresser
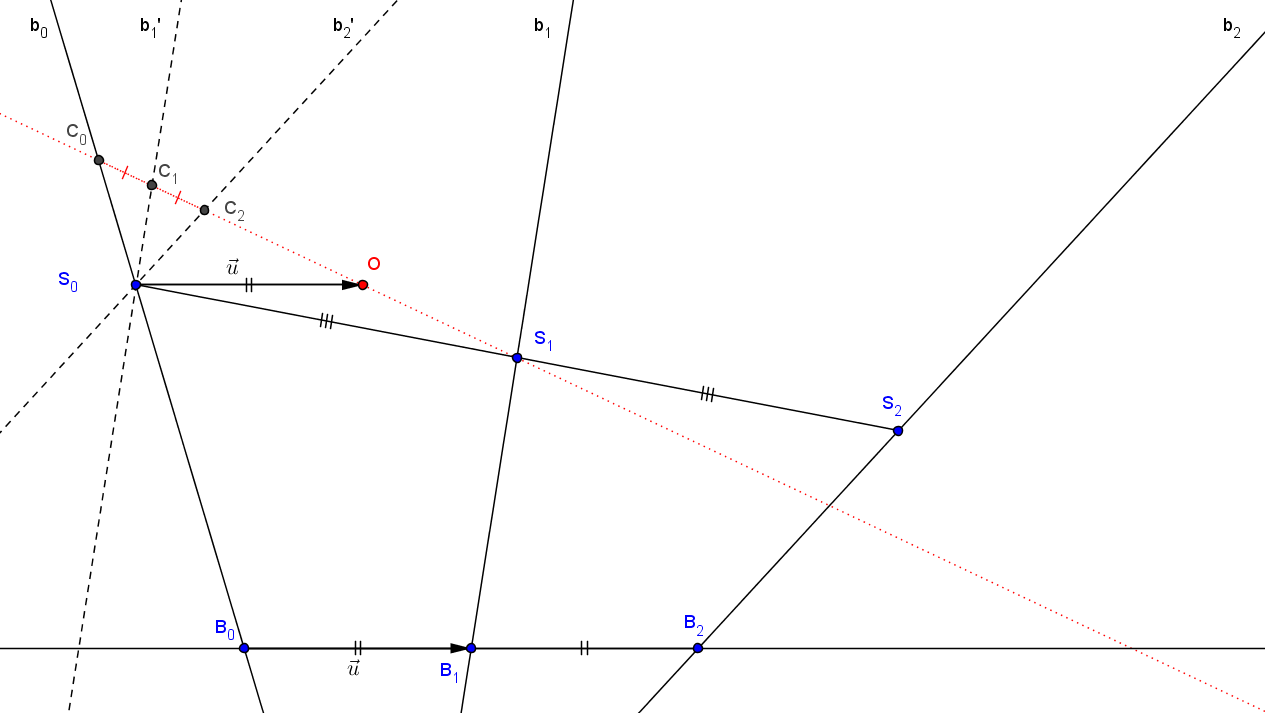
Quelqu'un saurait-il m'aider?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 11 Sep 2014, 18:48
par fatal_error » 11 Sep 2014, 18:48
salut,
je suis pas sûr de comprendre, sur ton dessin, il n'y a même pas S1+u qui appartient à (YZ)
Je ne comprends pas non plus pourquoi tu traces la parallèles à (YZ) passant par S1 si tu ne t'en sers pas (elle ne figure même pas sur l'image d'ailleurs)
la vie est une fête

-
Frednight
- Membre Rationnel
- Messages: 616
- Enregistré le: 04 Fév 2007, 17:03
-
 par Frednight » 11 Sep 2014, 18:59
par Frednight » 11 Sep 2014, 18:59
fatal_error a écrit: salut,
je suis pas sûr de comprendre, sur ton dessin, il n'y a même pas S1+u qui appartient à (YZ)
Je ne comprends pas non plus pourquoi tu traces la parallèles à (YZ) passant par S1 si tu ne t'en sers pas (elle ne figure même pas sur l'image d'ailleurs)
Effectivement je me suis complètement emmêlé. Toutes mes excuses : je voulais parler de la parallèle à
)
passant par

(j'ai corrigé dans l'énoncé ci-dessous). Normalement tout est ok mais n'hésitez pas à me signaler quoi que ce soit au moindre doute : je suis malheureusement assez coutumier de ce genre d'erreurs idiotes malgré mes relectures :marteau:
Frednight a écrit:Soient trois points
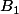
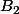
et
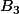
tels que
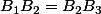
, et trois autres points


et
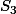
tels que

On note

(resp.
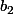
et
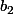
) la droite
)
(resp.
)
et
)
).
On trace la droite
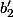
(resp.
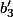
) la droite parallèle à
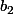
(resp.
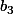
) et passant par

On trace une droite perpendiculaire à

en point qu'on nomme

. Cette droite coupe
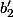
en un point que l'on nomme

.
On nomme

le point symétrique à

par

. La droite parallèle à

et passant par

coupe
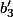
en un point

.
La droite
)
coupe

en un point

.
On trace la parallèle à
)
passant par

Je souhaiterais démontrer que la translation du point

par le vecteur
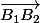
appartient à cette dernière droite parallèle à
)
passant par

mais je n'y parviens pas.
Je suppose que cela est en partie explicable par l'égalité

mais sans arriver à progresser

Quelqu'un saurait-il m'aider?
-
Frednight
- Membre Rationnel
- Messages: 616
- Enregistré le: 04 Fév 2007, 17:03
-
 par Frednight » 07 Oct 2014, 20:43
par Frednight » 07 Oct 2014, 20:43
Bon j'ai revu mon énoncé en espérant que celui-ci est désormais plus clair, d'autant que le problème subsiste.
Soient trois points
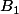
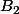
et
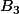
tels que
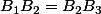
, et trois autres points


et
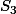
tels que

On note
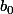
(resp.

) la droite
)
(resp.
)
).
On trace la droite
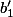
(resp.
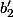
) la droite parallèle à

(resp.
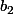
) et passant par

Je souhaiterais démontrer que la translation

du point
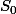
par le vecteur
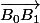
est telle que la droite
)
coupe les droites
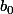
,
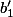
et
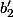
en trois points qui forment deux segments égaux

Quelqu'un saurait-il m'aider?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 07 Oct 2014, 22:18
par chan79 » 07 Oct 2014, 22:18
Salut
Tu devrais corriger l'énoncé au niveau des indices.
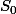
n'est pas défini ...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Oct 2014, 22:30
par Ben314 » 07 Oct 2014, 22:30
Salut,
JE PREND LES NOTATIONS DU DESSIN (qui ne sont pas les mêmes que celles du texte...

)
Il y a au moins une solution analytique (ohhhh, le GROS NUL !!!) pas trop compliqué
Dans le repère
)
on a
\ ;\ S_1:(1,0)\ ; \ S_2:(2,0)\ ; \ O:(\alpha+1,\beta)\ ;\ B_0:(0,1)\ ;\ B_1:(\alpha+1,\beta+1)\ ;\ B_2:(2\alpha+2,2\beta+1))
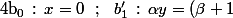x\ \ ;\ \ b'_2\,:\,\alpha y=(\beta+\frac{1}{2})x\ \ ;<br />\ \ (OS_1)\,:\, \alpha y=\beta (x-1))
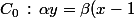=-\beta\,\longrightarrow\,(0,-\frac{\beta}{\alpha}))
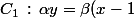=(\beta+1)x\,\longrightarrow\,(-\beta,-\frac{\beta(\beta+1)}{\alpha}))
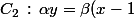=(\beta+\frac{1}{2})x\,\longrightarrow\,(-2\beta,-\frac{\beta(2\beta+1)}{\alpha}))
(en supposant

, c'est à dire
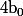
non parallèle à
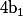
)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Frednight
- Membre Rationnel
- Messages: 616
- Enregistré le: 04 Fév 2007, 17:03
-
 par Frednight » 08 Oct 2014, 17:27
par Frednight » 08 Oct 2014, 17:27
Ben314 a écrit:Salut,
JE PREND LES NOTATIONS DU DESSIN (qui ne sont pas les mêmes que celles du texte...

)
Toutes mes excuses pour cette erreur. j'avais pourtant fait une relecture... je suis une vraie calamité :triste:
merci beaucoup pour ta réponse.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités

