Groupe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 19 Jan 2007, 22:52
par yos » 19 Jan 2007, 22:52
Voilà un exercice qu'on peut chercher dans le métro ou chez le coiffeur. Le genre qu'on devrait toujours avoir sur soi pour patienter quelquepart :
a et b sont dans un groupe et vérifient
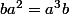
et
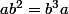
. Il faut prouver que a=b=1.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 19 Jan 2007, 23:05
par fahr451 » 19 Jan 2007, 23:05
mon coiffeur étant ponctuel j'ajoute que le groupe est commutatif.
-
mathelot
 par mathelot » 20 Jan 2007, 17:14
par mathelot » 20 Jan 2007, 17:14
donc

suffit.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 20 Jan 2007, 17:55
par yos » 20 Jan 2007, 17:55
mathelot a écrit:donc

suffit.
Qu'y-a-t-il à gauche du "donc"?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Jan 2007, 22:46
par yos » 21 Jan 2007, 22:46
Je fais remonter.
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 21 Jan 2007, 23:26
par BQss » 21 Jan 2007, 23:26
mathelot a écrit:donc

suffit.
Que le groupe soit commutatif ou pas de toute facon si a=b alors necessairement a=b=1.
Par contre je vois pas pourquoi le groupe est commutatif? C'est une donnée que tu as oubliée sans quoi ca ne marche pas c'est ca Yos?
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 21 Jan 2007, 23:50
par BQss » 21 Jan 2007, 23:50
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 22 Jan 2007, 11:49
par fahr451 » 22 Jan 2007, 11:49
REM : si le groupe est commutatif il n 'y a rien à faire, le résultat est évident,et je n'ai pas eu à faire patienter mon coiffeur.
Le seul cas intéressant est donc quand le groupe n'est pas supposé commutatif.
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 22 Jan 2007, 12:31
par BQss » 22 Jan 2007, 12:31
fahr451 a écrit:REM : si le groupe est commutatif il n 'y a rien à faire, le résultat est évident,et je n'ai pas eu à faire patienter mon coiffeur.
Le seul cas intéressant est donc quand le groupe n'est pas supposé commutatif.
ok c'est ce que je me disais aussi sur ta remarque. Prendre le groupe commutatif pour que ton coiffeur n'attende pas...
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 22 Jan 2007, 12:33
par BQss » 22 Jan 2007, 12:33
fahr451 a écrit:REM : si le groupe est commutatif il n 'y a rien à faire, le résultat est évident,et je n'ai pas eu à faire patienter mon coiffeur.
Le seul cas intéressant est donc quand le groupe n'est pas supposé commutatif.
mais c'est tout aussi evident si le groupe n'est pas commutatif...
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 22 Jan 2007, 12:37
par BQss » 22 Jan 2007, 12:37
fahr451 a écrit:REM : si le groupe est commutatif il n 'y a rien à faire, le résultat est évident,et je n'ai pas eu à faire patienter mon coiffeur.
Le seul cas intéressant est donc quand le groupe n'est pas supposé commutatif.
Mais c'est tout aussi evident si le groupe n'est pas commutatif....
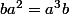
et
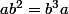
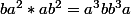
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 22 Jan 2007, 13:39
par BQss » 22 Jan 2007, 13:39
ok je l'ai mais c'est pas elegant du tout.
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 22 Jan 2007, 14:12
par BQss » 22 Jan 2007, 14:12
J'ai montré que b=1 <--> a=b
Cela revient donc a prouver que b=1.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 22 Jan 2007, 15:32
par yos » 22 Jan 2007, 15:32
coiffeur / commuta-tif c'était un jeu de mots?
Si ab=ba, le résultat est évident en effet.
Le groupe n'est pas supposé commutatif, je confirme.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 22 Jan 2007, 15:34
par fahr451 » 22 Jan 2007, 15:34
excellent yos :)
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 07 Fév 2007, 19:41
par Imod » 07 Fév 2007, 19:41
Après "quelques" manipulations j'ai réussi à montrer que le groupe engendré par a et b est égal à son groupe dérivé , je ne sais pas si cela apporte grand-chose ?
Imod
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 07 Fév 2007, 21:01
par allomomo » 07 Fév 2007, 21:01
Salut,
Je complète le défi :
Montrer que
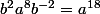
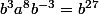
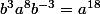
a partir de la seconde supposition
En déduire que
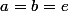
C'est un truc qu'on a eu en exercice ....
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 09 Fév 2007, 18:06
par Imod » 09 Fév 2007, 18:06
En m'inspirant des indications d'allomomo :
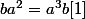
peut s'écrire
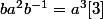
ou encore
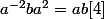
. De même
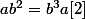
peut s'écrire
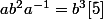
ou
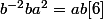
. En élevant [3] à la puissance 4 on obtient :
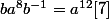
. Alors
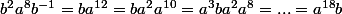
donc
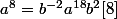
. Les relations [4] et [6] donnent :
^{19}=a^{-2}b^{19}a^2=a(ba)^{18}b=ab^{-2}a^{18}b^3)
c'est à dire
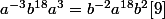
. Les relations [7] , [8] et [9] donnent
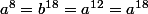
donc
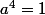
,
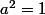
,
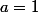
et
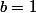
.
Je ne suis pas sûr que mon coiffeur apprécie le stock de brouillon que j'ai laissé dans sa poubelle :we:
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
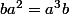 et
et 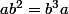 . Il faut prouver que a=b=1.
. Il faut prouver que a=b=1.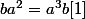 peut s'écrire
peut s'écrire 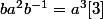 ou encore
ou encore 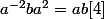 . De même
. De même 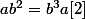 peut s'écrire
peut s'écrire 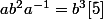 ou
ou 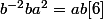 . En élevant [3] à la puissance 4 on obtient :
. En élevant [3] à la puissance 4 on obtient : 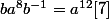 . Alors
. Alors 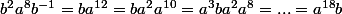 donc
donc 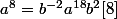 . Les relations [4] et [6] donnent :
. Les relations [4] et [6] donnent : ^{19}=a^{-2}b^{19}a^2=a(ba)^{18}b=ab^{-2}a^{18}b^3) c'est à dire
c'est à dire 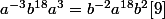 . Les relations [7] , [8] et [9] donnent
. Les relations [7] , [8] et [9] donnent 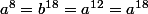 donc
donc 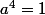 ,
, 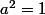 ,
, 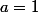 et
et 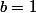 .
.