Fonctions usuelles dans R^2

par **barbu23** » 03 Fév 2012, 22:25

Bonsoir,

Les fonctions usuelles et leurs inverses dans

sont un peu nombreuses en analyse. Par exemple,

et

ou bien

et

ou bien

et

... etc.
Est ce qu'il existe un paquet de fonctions qu'on peut qualifier de "usuelles", mais, dans

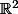
, et qu'on peut facilement construire leurs inverses, à part les endomorphismes et les applications affines ... ?

Merci d'avance. :happy3:

par **barbu23** » 03 Fév 2012, 23:30

Un peu d'aide svp. :happy3:

par **barbu23** » 04 Fév 2012, 00:05

Un peu d'aide svp. :happy3:

par **barbu23** » 04 Fév 2012, 15:07

Un peu d'aide svp. :happy3:

par **barbu23** » 04 Fév 2012, 16:29

Un peu d'aide svp. :happy3:

par **barbu23** » 04 Fév 2012, 23:55

svp, un peu d'aide :happy3:
J'en ai vraiment besoin. :happy3:

par **barbu23** » 05 Fév 2012, 16:16

Un petit up pour voir si quelqu'un a une réponse. :happy3:

par **barbu23** » 05 Fév 2012, 21:24

Un petit up pour voir si quelqu'un a une réponse. :happy3:
Merci d'avance. :happy3:

par **barbu23** » 06 Fév 2012, 15:04

Et moi ? Il n'y'a personne pour me répondre ? :cry:

par **barbu23** » 07 Fév 2012, 17:49

svp, j'ai besoin d'aide. :happy3:

par **Dlzlogic** » 07 Fév 2012, 19:13

barbu23 a écrit:svp, j'ai besoin d'aide. :happy3:

Bonjour,
Peut-être ce lien vous intéressera.
http://www.mathcurve.com/courbes2d/courbes2d.shtml

par **barbu23** » 07 Fév 2012, 21:36

Merci beaucoup :happy3:
mais ton lien ne contient pas d'exemples en

, de fonctions et de leurs inverses malheureusement. :happy3:

par **barbu23** » 13 Fév 2012, 20:06

Un peu d'aide svp. :happy3:

par **ksavier** » 13 Fév 2012, 20:15

je n'ai jamais rencontré un package de fonctions usuelles de

.

Il paraît naturel dans ce cas, d'envisager les fonctions complexes de la variable complexe (fonctions holomorphes donc)

Sans doute n'ai je pas compris la question posée.

par **barbu23** » 13 Fév 2012, 21:02

Non, tu as raison, je cherche un package de fonctions bijectives de la forme :

suivis de leurs inverses. :happy3:
Mais, je n'arrive pas à en trouver quelques unes. :happy3:

par **barbu23** » 14 Fév 2012, 19:03

Un peu d'aide svp. :happy3:
Je ne suis jamais tombé sur un exemple de fonctions

bijective et qui possède un inverse

bien déterminé. :happy3:

par **Dlzlogic** » 14 Fév 2012, 19:16

barbu23 a écrit:Un peu d'aide svp. :happy3:

Bonsoir,
J'ai pas l'impression que vous trouverez grand-chose d'autre.
Par ailleurs, je n'arrive pas à en imaginer l'utilité.

par **barbu23** » 14 Fév 2012, 19:22

Pourquoi ce n'est pas possible ?
Je suis curieux de découvrir quelques exemples de fonctions

bijectives qui admettent des inverses explicites et bien déterminés. :happy3:
Je suis sûr que c'est très important et qu'on peut leur trouver plusieurs applications en mathématiques. :happy3:
Je ne suis jamais tombé sur un exemple de fonctions

bijective et qui possède un inverse

bien déterminé.

par **ksavier** » 15 Fév 2012, 06:02

La géométrie peut donner des exemples, le groupe orthogonal

est rempli d'applications inversibles.

par **barbu23** » 15 Fév 2012, 14:08

ksavier a écrit:La géométrie peut donner des exemples, le groupe orthogonal est rempli d'applications inversibles.

Non, j'ai dit à part les endomorphismes et les applications affines. :happy3:

Fonctions usuelles dans R^2

Fonctions usuelles dans R^2

Qui est en ligne