Fonctions usuelles

[T-T]

bonjour :) j'ai un petit probléme sur un exo

j'ai f(x) = arcsin(2x/(1+x²))

Justifier que pour tout x appartenant a R on a 2|x|1+x²
Soit x R
(1-|x|)^2<=0 donc 1-2|x|+x²<=0 d'ou 2|x|<=1+x²

Précisez le domaine de définition

la fonction h(x)=2x/(1+x²) est définie sur R
On cherche alors les valeurs de x pour lesquelles f(x) [-1,1]

or d'après le question précédente on a pour tout x de R

-1< 2x/(1+x²)<1
donc f est définie sur R

justifier que la courbe Cf présente un centre de symétrie

on a f(-x)=-f(x) donc symétrie par rapport a l'origine.

pour t de ]-pi/2,pi/2[ simplifier 2tan t/(1+tan²t)

Soit t de]-pi/2,pi/2[ 2tan t/(1+tan²t)=sin(2t)

puis simplifier f(tan t )

donc on a f(tan t)=arcsin(sin(2t))

Exprimer , pour tout x de R ,f(x) a l'aide de g(x)=arcsin(sin2t) et arctan
Je n'ai pas réussi cette question
Pouriez vous me donner une indication ,
merci :)

[XENSECP]

arcsin(sin(2t)) sur l'intervalle donné de t, c'est pas trop dur !

[T-T]

ouais ^^ sa donne arcsin(sin2t)=2t sur cet intervalle mais c'est pas ce qu'on me demande

[XENSECP]

Oui j'avoue ^^
Euh je vois pas trop la question... tu mélanges x et t, j'y comprends plus grand chose ;)

[T-T]

ouais je vais essayer d'etre plus clair

j'ai la fonction g(x)=arcsin(sin(2t) définie sur R

et j'ai f(x)=arcsin(2x/1+x²) dont j'ai fais l'étude

et on me demande d'exprimer pour tout c de R

f(x) a l'aide des fonctions g et arctan

merci !

[T-T]

j'ai fais une faute de frappe , c'est pour tout x de R :s

[T-T]

s'il vous plait , personne pourrait me donner une indication :)

[mathelot]

s'il vous plait , personne pourrait me donner une indication

où l'on a posé

aux niveau des domaines, c'est plus compliqué car x=tan(u)
s'inverse sur
mais v=sin(2u) n'est pas injective et s'inversera localement.

faut donc regarder avec précaution.

[mathelot]

bonsoir,


soit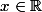 , on pose x=tan(u)

la (restriction de la) tangente à l'intervalle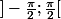 est une bijection indéfiniment dérivable ainsi que son application réciproque arctan.

un difféomorphisme.

grosso modo, on ne perd aucune généralité à travailler avec la variable x
ou la variable u.

dans ces conditions
f(x)=arcsin(sin(2u))

et

ces deux quantités ne peuvent pas être toujours égales

Il faut donc discuter selon
si
alors

si
alors

si
alors




remarques:
i) géométriquement,il s'agit de paramètrage local de la courbe constituée
du cercle. La différence entre les deux notions, c'est que le cercle
est un pauvre ensemble euclidien constitué de points à égale distance du centre, où la notion de courbure n'intervient pas directement,
tandis que la courbe, de support le cercle, a une structure de variété, localement paramétrable,avec un revêtement, donnés par l'exponentielle complexe


ii) on dispose donc d'un atlas, c'est à dire d'un recouvrement du cercle
par des ouverts topologiquement semblables à des intervalles.
et içi, on travaille avec les changements de cartes
on voit parfois des bizarreries comme des fonctions (globalement) impaires
dont la formule locale utilise arccos.

iii) pour s'en sortir pratiquement et faire les exos, y a une idée simple:
on ne travaille pas modulo mais bien au contraire par intervalles.