Diagonalisation d'une matrice

[couturierclaire]

ex1
Diagonaliser cette matrice (carrée):
( 1 1 1 1 1
1 1 0 0 0
1 0 1 0 0
1 0 0 1 0
1 0 0 0 1 )


Ex2
Diagonaliser cette matrice:
( ;)1² ;)1;)2 ;)1;)3 ;)1;)4 ;)1;)5
;)2;)1 ;)2² ;)2;)3 ;)2;)4 ;)2;)5
;)3;)1 ;)3;)2 ;)3² ;)3;)4 ;)3;)5
;)4;)1 ;)4;)2 ;)4;)3 ;)4² ;)4;)5
;)5;)1 ;)5;)2 ;)5;)3 ;)5;)4 ;)5² )



Pour l'exercice 1, après de longs calculs en utilisant cette formule: det(a-XI)=0, je suis tombé sur le résultat suivant: (1-X)(2X²-4X+1)=0
j'aimerais savoir si il est correct?

Pour l'exercice 2, je l'ai fait de la meme façon que l'exercice précédent, je l'ai pas terminé car j'ai trouvé que c'était super long et que je pense qu'il y a des astuces/ des méthodes afin de simplifer les calculs, quelqu'un pourrait t'il m'aider?

Merci d'avance

[zygomatique]

salut

déjà dire salut ... au moins ...

ensuite pourquoi mettre des parenthèses .... qui créent un décalage de colonne ...

enfin le degré de det (A - xI) est 5

....

quant à l'exercice 2 c'est illisible ... sans indice ....

[Ben314]

Salut,
Je ne sais pas quelle est la méthode attendue pour résoudre les deux exercices : Soit complètement "no brain" en appliquant à la lettre la méthode générale à appliquer à une matrice "quelconque", soit en utilisant un peu de bon sens vu les formes très particulières des matrices. Pour l'exercice 1, c'est plus ou moins discutable vu que, même à la bourrin, on va finir par y arriver, mais pour le 2, je souhaite bien du courage à celui qui refuse de réfléchir...

Exercice 1 :
Pour diagonaliser la matrice M, il suffit de diagonaliser (car 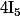est diagonale dans n'importe quelle base).
Or il est clair que l'image de N est de dimension 2, (engendrée par et ) donc le noyau est de dimension 3 et il est clair qu'il a pour base 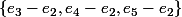: ça fait déjà un sous-espace propre de dimension 3 associé à la valeur propre 0 de N (c'est à dire à la valeur propre 1 de M).
Ensuite, on voit que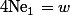 et 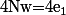ce qui implique que et que ce qui fournit deux valeurs propres/vecteurs propres supplémentaires.

Exercice 2 :
La matrice en question est en fait égale à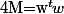 avec donc son image est de dimension 1 (engendrée par w) et son noyau est de dimension 4 (c'est l'ensemble des vecteurs orthogonaux à w) ce qui fourni immédiatement les sous espaces propres (lorsque l'image d'une application linéaire est de dimension 1, c'est évidement un sous-espace propre)