Bonjour,
Il est possible de faire un point aujourd'hui sur la recherche des nombres presque entiers de la forme
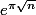
après essai de tous les entiers

de 1 à 1 million.
Vous trouverez dans le fichier excel joint une liste quasi exhaustive de ces derniers ayant une partie décimale commençant par une répétition d'au moins cinq fois le chiffre 9 ou cinq fois le chiffre 0.

On constate qu'une bonne proportion des entiers

(situés sous la racine) peuvent se réécrire sous la forme :
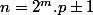
avec

entier et

premier.
Aujourd'hui, je m'intéresse au cas ou
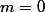
et plus précisément aux presque entiers de la forme
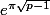
. Cela signifie que

est pair et la cerise sur le gâteau serait d'en trouver un qui soit un carré parfait (permettant ainsi de faire sauter la racine). Géométriquement cela reviendrait à trouver le diamètre d'un cercle tel que sa circonférence soit égale à
)
ou
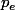
est un presque entier supérieur à 1 million.
Le deuxième défi consisterait à trouver un presque entier dont la partie décimale commencent par une répétition d'au moins douze fois le chiffre 9 ou douze fois le chiffre 0. Cela répondrait définitivement à la question : La constante de Ramanujan (cas ou
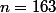
) est elle la seule à engendrer un presque entier de la forme
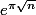
aussi proche d'un entier.
Le débat est ouvert pour le moment.
Lorsqu'on essai de réécrire
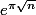
, il est possible d'obtenir quelquechose de la forme :
})
La fonction
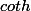
étant strictement supérieur à

(asymptote horizontale) on s'attend à ce que
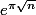
tende vers +inf mais cela ne donne aucune info sur la partie décimale de la chose.
C'est horriblement compliqué de trouver des valeurs de

qui génèrent des presque entiers très proches d'un entier. Cela semble échapper à toute formule simple (un peu comme les nombres premiers).
Aujourd'hui je sollicite les connaissances des membres du forum car ce problème me dépasse totalement.



