Partie entière et racine carrée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ttk
- Messages: 8
- Enregistré le: 28 Déc 2013, 15:29
-
 par ttk » 30 Déc 2013, 12:36
par ttk » 30 Déc 2013, 12:36
Je trouvais la méthode de Tiruxa très fine :
Tiruxa a écrit:On a
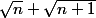
qui est élément de [p;p+1[ et aussi de
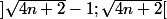
deux intervalles de longueur 1 qui ne sont pas disjoints puisque leur intersection contient
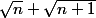
.
Mais là où j'ai un problème c'est que l'on peut avoir dans cet ordre :
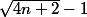
, p ,
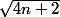
, p+1 et là ça marche.
mais on peut avoir aussi
p ,
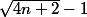
, p+1 ,
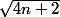
et là cela ne va plus du tout.
Pourquoi ce deuxième cas est il impossible ?
J'ai cherché à montrer l'impossibilité du cas n°2 en encadrant p avec n et en essayant de montrer que
p<
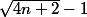
impossible ou p+1<
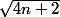
impossible mais pour l'instant je n'abouti pas. En fait ça revient toujours au même problème : montrer que
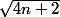
< p+1 quelquun a une idée ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 30 Déc 2013, 13:00
par chan79 » 30 Déc 2013, 13:00
la démo sur le site animath est claire:
s'il existait un entier

tel que
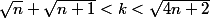
on aurait en élevant au carré
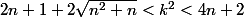
or, le membre de gauche est supérieur à 4n+1
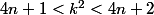
impossible
4n+2=2(2n+1) ne peut pas être un carré car 2n+1 serait pair
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 30 Déc 2013, 13:27
par nodjim » 30 Déc 2013, 13:27
Ouais là c'est court.
-
ttk
- Messages: 8
- Enregistré le: 28 Déc 2013, 15:29
-
 par ttk » 30 Déc 2013, 13:30
par ttk » 30 Déc 2013, 13:30
Très habile, merci chan79
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
qui est élément de [p;p+1[ et aussi de
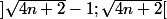
.
, p ,
, p+1 et là ça marche.
, p+1 ,
et là cela ne va plus du tout.
