Démonstration images réciproques

[eludante]

Bonjour, j'ai besoin d'aide pour démontrer ceci :

Il n'y a aucune autre information donnée, mais je pense que A est un ensemble quelconque et
Merci.

[L.A.]

Bonjour.

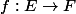
Etant donné une application et un ensemble , les éléments de E se répartissent en deux sous-ensembles, ceux dont l'image par f est dans A et les autres.

[eludante]

J'avais effectivement compris ça mais comment fait-on la démonstration ?
J'ai pensé qu'il fallait montrer que et que mais je ne sais pas comment m'y prendre.

[L.A.]

Prends un x dans et suppose qu'il est dans puis tires-en une contradiction.

Tu peux faire ça mais ce n'est pas le plus logique à mon avis.
Tu peux vérifier (ce qui revient au même) que


et en déduire que ces deux ensembles sont complémentaires l'un de l'autre dans E.

Quoiqu'il en soit, ça se fait en quelques lignes.

[eludante]

C'est bon de cette manière ? : Soit alors et or mais là je sais pas si il y a une inclusion entre deux ensembles ou une égalité

[L.A.]

Non, n'a pas de sens puisque qu'on a pas a priori d'hypothèse sur l'injectivité ou la surjectivité de f.

Attention, les deux ensembles dont tu veux montrer l'égalité sont des sous-ensembles de E et pas de F. Il faut donc considérer des éléments x de E.

En revanche ton égalité finale est bien une égalité.

[eludante]

Finalement, voilà ce que j'ai fais, en espérant que ce soit correct :



donc :


donc :

Finalement :

[L.A.]

Cela m'a l'air correct.

Dans la rédaction tu peux éliminer les assertions du type et (quand elles sont combinées à une autre assertion par un "et") puisqu'elles sont toujours vraies et n'apportent donc rien.

Tu peux même raisonner par équivalence directement plutôt que par double implication.

[eludante]

Ok, merci beaucoup !