Geometrie algebrique

[barbu23]

Bonsoir @lapras :

Je ne comprends pas ta question exactement. Tu veux savoir qu'est ce qu'une somme disjointe/un produit/un produit fibré/une somme amalgamée dans la catégorie des groupes ?
Attention le foncteur d'oubli Grp -> Ens ne commute pas nécessairement à la formation de ces opérations (ça commute au produit mais pas à la somme disjointe)

Je vais t'expliquer ce que je recherche de manière plus simple.
Quels sont parmi les objets de la catégorie des groupes que j'ai défini dans le message précédent :
Ceux qui représentent, par rapport à la catégorie des ensembles, la notion de produit fibré et ceux qui représentent la notion de somme amalgamée ? et ceux qui ne représentent ni l'une ni l'autre ? Que représentent -ils dans ce cas là ces derniers par rapport à la catégorie des ensembles ?
Le produit fibré et la somme amalgamée sont deux notions duales n'est ce pas ?
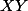
Quel est le dual de la notion de produit cartésien , dans la catégorie des ensembles ?
Merci d'avance. :happy3:

[lapras]

Bonsoir @lapras :

Je vais t'expliquer ce que je recherche de manière plus simple.
Quels sont parmi les objets de la catégorie des groupes que j'ai défini dans le message précédent :
Ceux qui représentent, par rapport à la catégorie des ensembles, la notion de produit fibré et ceux qui représentent la notion de somme amalgamée ? et ceux qui ne représentent ni l'une ni l'autre ? Que représentent -ils dans ce cas là ces derniers par rapport à la catégorie des ensembles ?
Le produit fibré et la somme amalgamée sont deux notions duales n'est ce pas ?
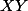
Quel est le dual de la notion de produit cartésien , dans la catégorie des ensembles ?
Merci d'avance. :happy3:

Ok je comprends maintenant : tu cherches à appliquer le foncteur d'oubli et voir ce que devient une opération dans la catégorie des ensembles.
La somme (amalgamée ou disjointe) ne correspond à rien dans la catégorie des ensembles : par exemple la somme disjointe de deux groupes A et B est l'ensemble des mots formels constitués de lettres de A et de B, avec des simplifications évidentes (e.g. xx^(-1)=e).
Le produit K x H correspond au produit ensembliste.
Le produit semi-direct n'a pas de sens catégorique : il n'y a pas un unique produit semi-direct (à iso près) en général.
En résumé : le foncteur d'oubli est très mauvais du point de vue de la somme, et est bien du point de vue du produit. Il est aussi bien du point de vue des limites (projectives, inductives).