Bonjour à tous,
Voilà j'ai un DM de Maths à rendre en fin de semaine, et il y a un exercice que je n'arrive pas à faire, pouvez-vous m'aider svp.
L'exercice c'est 1°) Résoudre dans C : (ro)² = -2i
2°) En déduire les solutions dans C de l'équation : z² + (5-3i)*z + 4-7i=0
Merci d'avance.
Exercice DM nombres complexes
9 messages
- Page 1 sur 1
Jo2395 a écrit:Merci de votre aide Carpate, mais cependant j'ai du mal à comprendre le calcul que vous avez effectué, pouvez-vous me décrire les étapes de vos calculs si cela ne vous dérange pas, je vous remercie.
C'est l'application du produit de 2 exponentielle : e^a e^b = e^(a+b)
On retrouve le cours (que tu sembles avoir oublié) :
Le produit de 2 nombres complexes est un complexe dont le module est le produit des modules et l'argument la somme des arguments (de ces 2 nombres)
Jo2395 a écrit:Merci de votre aide Carpate, mais cependant j'ai du mal à comprendre le calcul que vous avez effectué, pouvez-vous me décrire les étapes de vos calculs si cela ne vous dérange pas, je vous remercie.
Soit le complexe
Il a 2 racines carrées :
soit :
De même un complexe a 3 racines cubiques, n racines nièmes
Bonjour.
On peut aussi résoudre l'équation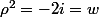 sous forme algébrique, l'argument du second peut ne pas être remarquable. En posant
sous forme algébrique, l'argument du second peut ne pas être remarquable. En posant 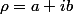 , on aura
, on aura 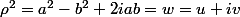 .
.
En séparant partie réelle et partie imaginaire, on obtient le sytème=u \\ 2ab=Im(w)=v \end{array}) , système qu'on peut résoudre aisément par la méthode de substitution. Le choix des signes de a et b est déterminé par le signe de leur produit donc celui de
, système qu'on peut résoudre aisément par la méthode de substitution. Le choix des signes de a et b est déterminé par le signe de leur produit donc celui de 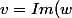)
On peut aussi résoudre l'équation
En séparant partie réelle et partie imaginaire, on obtient le sytème
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
