Limite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 27 Aoû 2006, 15:30
par nada-top » 27 Aoû 2006, 15:30
super_teufel a écrit:x-x= 0 ... il est ou le probleme.. ( tu le sait là que x=x ) ex. 6-6=0 100-100=0 , 1000000000000000000000000000000-100000000000000000000000000000000=0
alors la vraiment sans commentaire :hum: :hum: pour qui tu me prends !!!
il faudrait quand meme lire ce qu'a dit Sdec25
''on peut pas adittioner les équivalents''PS : je sais pas faire l'addition comme tu dis mais je m'endoute fort que
super_teufel a écrit:1000000000000000000000000000000-100000000000000000000000000000000=0
:lol4:
-
theorie
- Membre Naturel
- Messages: 27
- Enregistré le: 05 Fév 2006, 11:00
-
 par theorie » 27 Aoû 2006, 16:12
par theorie » 27 Aoû 2006, 16:12
Bon ben si ajouter des equivalents vous pose probleme:
} - \sqrt[4]{x^4(1 + 1/x^4)} = x\sqrt[3]{1 + 1/x^3} - x\sqrt[4]{1 + 1/x^4})
(J'ai factorisé à l'intérieur des racines par le terme de plus haut degré)
Vu que
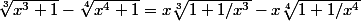
(l'égalité que je viens de montrer juste avant)
Vous êtes d'accord que
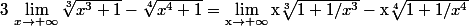
(j'ai pas fait d'adition d'équivalent ni rien là d'accord? Donc c'est bon)
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 27 Aoû 2006, 16:14
par nada-top » 27 Aoû 2006, 16:14
theorie a écrit:(j'ai pas fait d'adition d'équivalent ni rien là d'accord? Donc c'est bon)
ben je crois pas
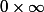
est une forme indeterminée .
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 27 Aoû 2006, 16:15
par nekros » 27 Aoû 2006, 16:15
Comme pourra te le confirmer nade-top, c'est exactement ce que j'avais fais (post supprimé)
Le problème, c'est qu'on aboutit à la forme indéterminée

A+
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 27 Aoû 2006, 16:18
par Sdec25 » 27 Aoû 2006, 16:18
Démontrons que 0=1 :
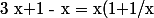 - x)
ce qui tend vers 0, donc 0=1
Où est l'erreur ? on ne peut pas dire que x(1+1/x) est de plus en plus proche de x.
(cf post 25)
Les équivalents sont à utiliser avec précaution. Dire que le quotient tend vers 1 ne veut pas dire que la différence tend vers 0.
On peut interpréter graphiquement (pour des fonctions qui tendent vers l'infini): la différence entre 2 fonctions tend vers 0 si les 2 courbes tendent à se confondre.
Le quotient tend vers 1 si la distance entre les courbes devient négligeable par rapport à la "hauteur" de la courbe.
-
theorie
- Membre Naturel
- Messages: 27
- Enregistré le: 05 Fév 2006, 11:00
-
 par theorie » 27 Aoû 2006, 16:21
par theorie » 27 Aoû 2006, 16:21
pourquoi 0* +infini??? je comprends pas....
les racines donnes 1, donc ça donne x*1
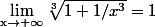
non??
même chose pour
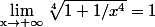
Sdec25 a écrit: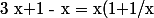 - x)
ce qui tend vers 0
D'où sorts-tu ça?? Pourquoi affirmes-tu que ça tends vers 0??
Et puis j'vois pas où tu vois des équivalents dans mon truc, j'ai juste factorisé...
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 27 Aoû 2006, 16:23
par nekros » 27 Aoû 2006, 16:23
1-1=0
A+
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 27 Aoû 2006, 16:24
par nekros » 27 Aoû 2006, 16:24
Oui mais 1-1=0 :lol4:
D'où le problème et la forme indéterminée
A+
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 27 Aoû 2006, 16:27
par nada-top » 27 Aoû 2006, 16:27
theorie----
= \lim_{x \to +\infty} x \;\times \lim_{x \to +\infty} \sqrt[3]{1+1/x^3} - \sqrt[4]{1+1/x^4} ) = +\infty \times 0)
!!
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 27 Aoû 2006, 16:37
par Sdec25 » 27 Aoû 2006, 16:37
theorie a écrit:D'où sorts-tu ça?? Pourquoi affirmes-tu que ça tends vers 0??
Et puis j'vois pas où tu vois des équivalents dans mon truc, j'ai juste factorisé...
J'affirme (mais c'est faux) que ça tend vers 0 car 1-1=0
Additionner les équivalents et multiplier 0 par l'infini ça revient au même dans ce cas, donc il faut faire attention.
Ce qu'il faut voir, c'est comment ça tend vers 0.
Si f tend vers 0 plus vite que 1/x alors xf tend vers 0.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
