Limite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 27 Aoû 2006, 00:23
par nada-top » 27 Aoû 2006, 00:23
[FONT=Palatino Linotype]
Salut , (eh oui c'est moi encore :lol5: )
voilà maintenant je travaille sur les limites et j'ai un probleme avec celle-ci :[/FONT] [FONT=Palatino Linotype]j'sais pas comment lever l'indetermination , muliplier par le conjugué mais j'ai pas la meme puissance ? changement de variable poser[/FONT]
[FONT=Palatino Linotype]j'sais pas comment lever l'indetermination , muliplier par le conjugué mais j'ai pas la meme puissance ? changement de variable poser[/FONT]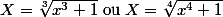
??
[FONT=Palatino Linotype]Merci[/FONT] :lol3:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 27 Aoû 2006, 00:33
par nekros » 27 Aoû 2006, 00:33
Salut,
Oublie ce que j'ai dis, je suis fatigué :lol3:
Je ne sais pas ce que ça vaut, mais en écrivant
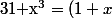(1-x+x^2))
?
Bonne nuit.
PS : très jolie l'écriture, c'est quoi comme police ?
A+
EDIT : pour ceux qui veulent suivre, j'avais abouti(?) à
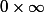
:briques:
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 27 Aoû 2006, 00:41
par kazeriahm » 27 Aoû 2006, 00:41
meme si le résultat est juste (on a des outils après bac :we: ) je crois que tu n'as pas levé l'indetermination pour un éleve de lycée (je pense ?!) puisque parallement au facteur qui tend vers 0, x tend vers l'infini...
enfin je dis ca, je dis rien :happy2:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 27 Aoû 2006, 00:41
par nada-top » 27 Aoû 2006, 00:41
salut
désolée mais
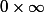
est une forme indterminée :hein:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 27 Aoû 2006, 00:44
par nekros » 27 Aoû 2006, 00:44
Arf oui vous avez raison...
Je cherche.
A+
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 27 Aoû 2006, 00:57
par nekros » 27 Aoû 2006, 00:57
Bof, ça revient au même...
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 27 Aoû 2006, 01:30
par nada-top » 27 Aoû 2006, 01:30
Re,
je ne vois pas ou ça peut ne ramener
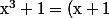 (x^2 -x+1))
mais bon je vais chercher encore.
PS : Nekros -- regarde ta signature :lol4: ([FONT=Palatino Linotype]c'est palatino Linotype [/FONT] )
Bonne nuit ! :lol3:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 27 Aoû 2006, 01:31
par nekros » 27 Aoû 2006, 01:31
nada-top a écrit:PS : Nekros -- regarde ta signature :lol4: ([FONT=Palatino Linotype]c'est palatino Linotype [/FONT] )
Je suis vraiment fatigué, bonne nuit !
A+
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 27 Aoû 2006, 01:45
par nekros » 27 Aoû 2006, 01:45
Arf, je crois avoir trouvé :

Or,

et

tendent vers

.
Donc le "tout" tend clairement vers

lorsque

tend vers
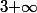
.
Donc en prenant le

, on trouve que la limite vaut
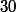
.
A+
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 27 Aoû 2006, 01:52
par Sdec25 » 27 Aoû 2006, 01:52
J'ai essayé de montrer que comme
)
, dans

le "1" on s'en fout, mais c'est pas si évident à montrer :ptdr:
peut-être une solution :
en utilisant
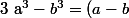(a^2+ab+b^2))
^{2/3}+x^2 + x\sqrt[3]{1+x^3} }<br />= \frac{1}{(1+x^3)^{2/3}+x^2 + x\sqrt[3]{1+x^3} })
équivaut au voisinage de
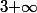
à

Donc
)
(asymptote oblique y=x)
De même
)
 - \epsilon_2(x) \longrightarrow 0)
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 27 Aoû 2006, 01:54
par nada-top » 27 Aoû 2006, 01:54
:doh: :doh: c'est quoi ça ??... je crois pas que c'est ce qui est demandé d'un élève qui n'a jamais étudié les fonctions exponentielles si c'est bien ça .
ça m'a l'air trés simple mais surement il y a une autre methode.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 27 Aoû 2006, 01:55
par nekros » 27 Aoû 2006, 01:55
nada-top a écrit::doh: :doh: c'est quoi ça ??... je crois pas que c'est ce qui est demandé d'un élève qui n'a jamais étudié les fonctions exponentielles si c'est bien ça .
ça m'a l'air trés simple mais surement il y a une autre methode.
:ptdr: :ptdr:
C'est pour ça que je l'ai retiré. Désolé j'avais pas vu ton post.
C'est dur de trouver des méthodes abordables au lycé lorsqu'on a vu les notions de petits o, développement limités, asymptotiques...
A+
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 27 Aoû 2006, 02:00
par nekros » 27 Aoû 2006, 02:00
Sdec25 a écrit: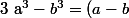(a^2+ab+b^2))
Je me doutais bien que ça servirait à quelque chose :ptdr:
A+
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 27 Aoû 2006, 02:02
par nada-top » 27 Aoû 2006, 02:02
Salut Sdec25,
alors la c'est trop , franchement je vois rien d'abord je passe sans commentaire sur ça o(x) :doh:
ensuite c'est quoi tout ces epsilon ?! quelle(s) proprité(s) tu as appliqué ? :hein:
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 27 Aoû 2006, 02:19
par Sdec25 » 27 Aoû 2006, 02:19
Salut
f=o(g) ou f0
 = 0)
nekros > merci, j'avais essayé de montrer que

sans succès et tu m'a donné l'idée d'utiliser une identité remarquable :zen:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 27 Aoû 2006, 02:27
par nada-top » 27 Aoû 2006, 02:27
on a
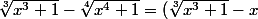-( \sqrt[4]{x^4 + 1}-x) =)
à ce qu'a trouvé Sdec25 et la meme chose pour

et puisque la limite des deux quotients vaut 0 l'orsque x tend vers

, on en déduit que la limite de l'epression vaut 0 .
(peut etre c'est ce que tu as fait Sdec25 mais j'ai pas compris tes notations:ptdr: )
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 27 Aoû 2006, 02:37
par Sdec25 » 27 Aoû 2006, 02:37
(J'ai répondu juste avant ton post)
epsilon(x) veut dire "fonction qui tend vers 0"
L'expression du dessus signifie donc :
(x + fct qui tend vers 0) - (x+fct qui tend vers 0) = fct qui tend vers 0
d'où
et puisque la limite des deux quotions est 0 l'orsque x tend vers

, on en déduit que la limite de l'epression vaut 0
:lol3:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 27 Aoû 2006, 02:47
par nada-top » 27 Aoû 2006, 02:47
ok merci Sdec25 et Nekros :++: c'est trés claire .
bonne nuit!! :lol3:
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 27 Aoû 2006, 02:49
par Sdec25 » 27 Aoû 2006, 02:49
de rien :happy3:
Et tu verras les epsilon(x) et o(x) en voyant les développement limités normalement :we:
bonne nuit :happy2:
-
super_teufel
- Membre Naturel
- Messages: 59
- Enregistré le: 21 Juil 2006, 01:54
-
 par super_teufel » 27 Aoû 2006, 05:02
par super_teufel » 27 Aoû 2006, 05:02
Ouais, mais c'est évident que

tend vers 1 quand x tend vers l'infini
Voilà le développement

=
})
On Fait tendre x vers l'infini donc 1+1/(x^a) = 1
donc cela devient
})
Hey je croit que tu comprend le reste

Il est tard , peut etre ai-je mal compris la question ,car il me semble que le probleme est simple: il tend vers 0!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
