Des urnes et des billes

[LA solution]

Bonjour, tout le monde jai un petit exo qui me fatigue sur ceux si je peux avoir votre aide ça me ferra du bien
Exo: Des urnes et des billes
Trois urnes contiennent des billes.
Chaque urne est suffisamment grande pour contenir la totalite des billes.
La seule operation autorisee est de doubler le nbre de billes contenues dans une urne en prelevant des billes dans une autre.
Demontrer qu il est possible, quel que soit la configuration initiale,d obtenir une configuration ou L'une des urnes est vide

[nodjim]

En prélevant dans une seule autre ?

[LA solution]

Oui, En prélevant des billes dans une autre

[nodjim]

Si aEt c'est fini.
Si a=b mettre tout a dans b et c'est fini.

[LeJeu]

Si a<b<c, il te suffit de vider tout a et une partie de c dans b.
Et c'est fini.
Si a=b mettre tout a dans b et c'est fini.

c'est donc qu'il ne faut faire le transvasement que d' UNE urne à l'autre
bien tenté nodjim..

[LA solution]

J ai mal compris ou vous voulez me dire par ex:si a=4, b=5 et c=7 on vide tout a cad de prendre les 4dans a+ 3dans5 pour obtenir 7?
ensuite de mettre 7dans c donc c devient 14

[chan79]

c'est donc qu'il ne faut faire le transvasement que d' UNE urne à l'autre
bien tenté nodjim..

par exemple
2-5-9
4-3-9
4-6-6
4-12-0

[nodjim]

Si on ne peut prélever que dans une seule urne, on est bloqué avec des configurations telles que 2,3,4, ou 3,4,5, ou 4,5,6 par exemple.

[chan79]

Si on ne peut prélever que dans une seule urne, on est bloqué avec des configurations telles que 2,3,4, ou 3,4,5, ou 4,5,6 par exemple.

pas sûr...
2-3-4
4-1-4
8-1-0

[nodjim]

Oui , j'ai vu ça en finissant d'écrire...
ça complique le problème.

[LeJeu]

Oui , j'ai vu ça en finissant d'écrire...
ça complique le problème.

ça créé le problème......

[LA solution]

j ai remarque qu' a trois nbres d objets consecutifs on onbtient la configuration demandee au 3ém prelevement

[Imod]

Bonsoir :zen:

J'ai déjà vu ce problème , il y a une solution assez simple et non calculatoire utilisant les écritures binaires des nombres de billes de chaque urne .

Je vous laisse y réfléchir .

Imod

[nodjim]

Je me doutais bien que ce problème allait attirer infailliblement Mr Imod. Bonjour à toi.

Peut être en partant de la situation finale, c'est à dire de la somme partagée en 2, dont l'une au moins est paire, conduit à toutes les combinaisons possibles de partage en 3.
Par exemple 9=1+8=3+6=5+4=7+2, chacune de ces config conduisant à au moins 1 config à 3 termes
1+8--->1 4 4 ----> 1 2 6 et 2 3 4---->
etc...

[LA solution]

Bonsoir,je n ai pas compris( 1+8--->1 4 4 ----> 1 2 6 et 2 3 4---->
etc...)explique moi svp

[nodjim]

Comme la règle proposée est de doubler un nombre dans une urne en piochant dans une autre, la suite au rebours, en partant d'une situation cible à 2 seules urnes, est de diviser par 2 un nombre pair de billes dans une urne et de transférer la moitié dans une autre urne. Si on arrive à prouver que l'ensemble des combinaisons à 2 urnes (S/2, si S est la somme totale des billes) conduit à toutes les configurations à 3 urnes, alors on aura gagné. Cette possibilité passe aussi peut être par une récurrence.
Pour l'instant je ne sais pas si la solution d'Imod en binaire consiste à trouver la bonne démarche pour arriver au but, quelle que soit la configuration de départ, ou bien si c'est une solution plus généraliste qui englobe tous les cas en une seule fois.

[Imod]

En fait l'indice que j'ai donné est un peu pourri :hum:

On utilise plutôt une division euclidienne puis une écriture binaire du quotient .

Un indice plus précis , on suppose par l'absurde ( en espérant que Léon n'est pas là ) qu'on ne peut vider aucune urne et on considère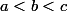 les contenus des trois urnes avec minimal . Ensuite il faut regarder ce qu'on peut faire avec l'écriture binaire du quotient de par .

La méthode est constructive :we:

Imod

[nodjim]

ça fait un bon bout de temps que je suis là dessus et je ne trouve pas. Quelqu'un d'autre a tenté ? Imod, le calculatoire, je veux bien, mais quel calcul ? L'enquête piétine...

[Imod]

J'ai un peu raté le dernier message , il faut dire que je vais rarement dans le supérieur et , ce qui n'arrange pas les choses , je n'avais plus d'adresse Email :hum:

On range les urnes en ordre croissant et on note 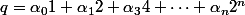le quotient euclidien de par . Puis au rang on déplace le contenu de l'urne de vers si 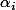est nul ou de vers dans le cas contraire . Après manipulations , est inférieur à et c'est fini .

Imod

[nodjim]

Je vois: tu pourras arriver à 1, mais es tu sûr qu'il y a assez de billes dans c pour terminer ?