Limite avec une racine

par **Ramanujan71** » 10 Déc 2012, 17:59

Bonsoir,
Comment prouver que

?
Ce n'est pas un polynome, on ne peut aussi pas utiliser le theoreme de comparaison,le conjugue...

Comment faire? Merci de m'aider :we:

par **leon1789** » 10 Déc 2012, 18:06

factorise l'expression par x

par **Ramanujan71** » 10 Déc 2012, 18:08

Factoriser par x? Comment?

par **leon1789** » 10 Déc 2012, 18:15

exemple

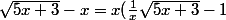essaie de voir ce que tu peux faire avec

quand x tend vers +infini

par **Ramanujan71** » 10 Déc 2012, 18:17

leon1789 a écrit:exemple

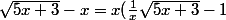essaie de voir ce que tu peux faire avec quand x tend vers +infini

Ok merci :we:

par **hammana** » 10 Déc 2012, 22:46

Ramanujan71 a écrit:Bonsoir,
Comment prouver que ?
Ce n'est pas un polynome, on ne peut aussi pas utiliser le theoreme de comparaison,le conjugue...

Comment faire? Merci de m'aider :we:

La méthode classique consiste à multiplier numérateur et dénominateur par la quantité conjuguée pour opbtenir

)). En divisant haut et bas par x on voit que la fraction tend vers -x

par **sta-love** » 10 Déc 2012, 23:25

J'aurais fais la même chose que hammana.
Le terme conjugué de f(x).
C'est à dire ça :

Après tu développe le numérateur puis tu trouve quelque chose comme a²-b² ou tu simplifiera avec le dénominateur.
Fais ton calcul et après je reviens te voir.

@leon1789 : Les termes prépondérants sont fait pour les polynôme et non les radicaux

par **leon1789** » 11 Déc 2012, 10:49

sta-love a écrit:@leon1789 : Les termes prépondérants sont fait pour les polynôme et non les radicaux

Que ce ne soit pas un polynôme, ça change quoi en fait ? rien me semble-t-il.

La factorisation par un facteur "bien choisi" est une méthode assez générale : ici quand on factorise par x, on tombe sur une limite du type

et on peut conclure.

sta-love a écrit:J'aurais fais la même chose que hammana.
Le terme conjugué de f(x).
C'est à dire ça :

Après tu développe le numérateur puis tu trouve quelque chose comme a²-b² ou tu simplifiera avec le dénominateur.
Fais ton calcul et après je reviens te voir.

D'ailleurs, une fois que vous utilisez l'expression conjuguée, développé et simplifié, vous allez tomber sur une fraction dont la limite est indéterminée

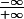
: comment trouver (et prouver) la limite de la fraction ? (...sans identifier les termes prépondérants aux numérateur et/ou dénominateur... :lol3: )

Limite avec une racine

Limite avec une racine

Qui est en ligne