Champ vectoriel F
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kti13
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Oct 2012, 12:42
-
 par kti13 » 01 Oct 2012, 12:44
par kti13 » 01 Oct 2012, 12:44
Soit un champ vectoriel F, donné par F = (z+y)i + xj + yk
a)Calculer sa divergence
b) Calcul rotF
Je comprend absolument rien...
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 01 Oct 2012, 12:49
par arnaud32 » 01 Oct 2012, 12:49
-
kti13
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Oct 2012, 12:42
-
 par kti13 » 01 Oct 2012, 12:52
par kti13 » 01 Oct 2012, 12:52
Oui merci j'ai deja lu pas mal de chose la dessus mais je sais même pas par ou commencer

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 01 Oct 2012, 12:58
par ampholyte » 01 Oct 2012, 12:58
kti13 a écrit:Oui merci j'ai deja lu pas mal de chose la dessus mais je sais même pas par ou commencer
Bonjour,
Tu as F = (z+y)i + xj + yk
Par définition de la divergence on sait que :
 = \frac{\delta{F_x}}{\delta x} + \frac{\delta{F_y}}{\delta y} + \frac{\delta{F_z}}{\delta z})
Pour calculer chaque membre il faut que tu considères les autres comme constant. Par exemple ici x ne dépend pas de y et de z donc la dérivé partielle de y = 0 idem pour la dérivée partielle de z + y ect...
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 01 Oct 2012, 13:01
par arnaud32 » 01 Oct 2012, 13:01

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 01 Oct 2012, 13:02
par ampholyte » 01 Oct 2012, 13:02
edit : Fait :D
-
kti13
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Oct 2012, 12:42
-
 par kti13 » 01 Oct 2012, 13:19
par kti13 » 01 Oct 2012, 13:19
Dons sa peut donner un truc dans ce genre ... ?
dif (F) = ((z+y) / x) + (x / y) + (y / z)
Excusez-moi je comprend rien j crois...
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 01 Oct 2012, 13:24
par arnaud32 » 01 Oct 2012, 13:24
sais tu ce qu'est une derivee? une derivee partielle?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 01 Oct 2012, 13:25
par ampholyte » 01 Oct 2012, 13:25
kti13 a écrit:Dons sa peut donner un truc dans ce genre ... ?
dif (F) = ((z+y) / x) + (x / y) + (y / z)
Excusez-moi je comprend rien j crois...
Pour faire simple :
}{dt})
est le calcul de la dérivée de la fonction u(t) par rapport à t
}{\delta x})
est le calcul de la dérivée PARTIELLE de la fonction u(x,y,z) (fonction à plusieurs variables) par rapport à x.
Exemple :
Si on suppose la fonction u(t) = t² + 3t + 1 alors sa dérivée est
}{dt} = 2t + 3)
Si maintenant on a une fonction u(x,y,z) = x + 2y + 3z alors sa dérivée partielle par rapport à x est
}{\delta x} = 1)
}{\delta y} = 2)
par rapport à y
}{\delta z} = 3)
par rapport à z
Plus compliqué :
u(x,y) = xy alors sa dérivée partielle par rapport à x est
}{\delta x} = y)
}{\delta y} = x)
par rapport à y
Est-ce plus clair ?
-
kti13
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Oct 2012, 12:42
-
 par kti13 » 01 Oct 2012, 13:25
par kti13 » 01 Oct 2012, 13:25
arnaud32 a écrit:sais tu ce qu'est une derivee? une derivee partielle?
Un dérivée oui, un dérivée partielle c'est ou on dérive mais que les x ou les y par exemple

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 01 Oct 2012, 13:29
par ampholyte » 01 Oct 2012, 13:29
kti13 a écrit:Un dérivée oui, un dérivée partielle c'est ou on dérive mais que les x ou les y par exemple
cf. au dessus
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 01 Oct 2012, 13:30
par arnaud32 » 01 Oct 2012, 13:30
-
kti13
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Oct 2012, 12:42
-
 par kti13 » 01 Oct 2012, 13:46
par kti13 » 01 Oct 2012, 13:46
Donc:
Div (F) =



Div (F) = 0 + 1 + 1 = 2 ?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 01 Oct 2012, 13:51
par ampholyte » 01 Oct 2012, 13:51
kti13 a écrit:Donc:
Div (F) =



Div (F) = 0 + 1 + 1 = 2 ?
C'est ça si tu as bien compris tu peux retourner faire le calcul sur ton exercice.
-
kti13
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Oct 2012, 12:42
-
 par kti13 » 01 Oct 2012, 13:52
par kti13 » 01 Oct 2012, 13:52
ampholyte a écrit:C'est ça as-tu bien compris ?
Oui merci après un temps de réflexion je viens de comprendre la divergence, je passe maintenant à la rotation

-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 01 Oct 2012, 13:53
par arnaud32 » 01 Oct 2012, 13:53
kti13 a écrit:Donc:
Div (F) =



Div (F) = 0 + 1 + 1 = 2 ?
non tu dois calculer
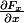
,

et
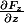
moi je t'ai donne en exemple
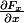
,
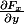
et

ici tu as div(F)=0+ 0 +0 = 0
-
kti13
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Oct 2012, 12:42
-
 par kti13 » 01 Oct 2012, 13:57
par kti13 » 01 Oct 2012, 13:57
rot (F) = DET ( i j k )
( a /ax a / ay a/az )
(Fx Fy Fz )
C'est bien ça ?
-
kti13
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Oct 2012, 12:42
-
 par kti13 » 01 Oct 2012, 13:58
par kti13 » 01 Oct 2012, 13:58
arnaud32 a écrit:non tu dois calculer
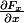
,

et
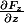
moi je t'ai donne en exemple
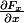
,
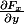
et

ici tu as div(F)=0+ 0 +0 = 0
Qui a raison du coup la ? je comprend plus rien
-
kti13
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Oct 2012, 12:42
-
 par kti13 » 01 Oct 2012, 14:17
par kti13 » 01 Oct 2012, 14:17
arnaud32 a écrit:non tu dois calculer
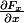
,

et
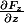
moi je t'ai donne en exemple
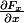
,
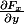
et

ici tu as div(F)=0+ 0 +0 = 0
Donc pour F = (z+y) i + xj + yk
div (F) = 1 + 2 + 1 ??????????
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 01 Oct 2012, 14:27
par arnaud32 » 01 Oct 2012, 14:27
kti13 a écrit:Donc pour F = (z+y) i + xj + yk
div (F) = 1 + 2 + 1 ??????????
tu prends
 = F_x(x,y,z)\vec{ i} + F_y(x,y,z) \vec{ j} + F_z(x,y,z) \vec{k})
tu peux calculer les 9 fonctions suivantes:
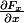
,
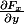
,
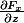
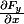
,
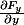
,
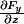
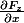
,
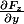
,
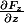
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
