Champ vectoriel V et divergence rotationnelle.

[novicemaths]

Bonsoir

Voici l'énoncé.

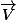
Montrer que quel que soit le champ on a div









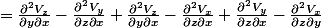
Est-ce que mes calculs sont corrects ?

A Bientôt

[issoram]

Bonsoir,

Non il y a une erreur à la deuxième composante de ton rotationnel: c'est l'opposé.
Du coup, les dérivées partielles secondes s'annulent bien 2 à 2
Sinon, tu as oublié de taper div à la deuxième ligne

[tournesol]

il s'agit de "nabla scalaire (nabla vectoriel V)" ie le produit mixte "det(nabla,nabla,V)" qui est évidement nul.
Mon raisonnement est douteux et je m'adresse à GaBuZoMeu .
C'est comme si je démontrais le th de Cayley Hamilton en écrivant "det(A-AI)=0"

[GaBuZoMeu]

Bonjour,
Pas de problème ici, c'est le formalisme des opérateurs vectoriels.
On peut aussi l'appliquer (c'est un peu plus délicat) pour calculer avec la fomule du double produit vectoriel.

[tournesol]

Bonsoir et merci GaBuZoMeu .

[novicemaths]

Bonsoir

Merci issoram, je n'avais pas compris qu'il fallait intervertir, au cas où il y aurait une quatrième, sixièmes ligne etc. J'aurais dû aussi faire l'opposé dans le rotationnel ?

A bientôt

[GaBuZoMeu]

Il ne faut pas "intervertir", il faut bien respecter la définition du rotationnel. Quand tu as écris la première ligne, c'est facile : tu écris les suivantes en appliquant une permutation circulaire sur .
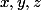
Et il n'y a pas de quatrième, sixième etc. car le rotationnel est un opérateur pour la dimension 3.
Petit détail : quand ta formule s'affiche tout petit comme ci-dessus, mets une commande \large ou \Large devant ; ça facilitera la lecture.