Petit exercice nombres complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Noisetteham
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Mai 2012, 12:38
-
 par Noisetteham » 30 Sep 2012, 18:49
par Noisetteham » 30 Sep 2012, 18:49
annick a écrit:Bonjour,
pour ma part, je ne me serai pas embrouillée avec les z barre.
Tu sais que M appartient à C, donc les coordonnées de M vérifient l'équation de C, soit
M(x, x/x-1).
Donc z=x+i(x/x-1)
Ensuite, tu calcules z² et tu remplaces tout ça dans Z=z²-2(1+i)z.
En principe, si M' appartient à l'axe de x, tu dois trouver un résultat réel, c'est-à-dire que la partie imaginaire est nulle(il n'y a plus de i dans ton équation).
Et oui, pour répondre à ta question, les calculs sont un peu longs, mais avec de la méthode, tu arriveras au bout.
Pourquoi je calcule z²?
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 30 Sep 2012, 18:51
par annick » 30 Sep 2012, 18:51
C'est exactement l'intérêt de ce forum, ptitnoir, c'est que chacun avec notre bagage, nous abordons les problèmes différemment et qu'ainsi les élèves ont à leur portée différentes manières d'atteindre le but recherché. Moi, cela me plaît beaucoup cette ouverture. :lol3:
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 30 Sep 2012, 18:53
par annick » 30 Sep 2012, 18:53
Tu calcules z² car tu as z² dans ta formule ( Z=z²-2(1+i)z) et qu'à un moment il va bien falloir le calculer !
-
Anonyme
 par Anonyme » 30 Sep 2012, 21:07
par Anonyme » 30 Sep 2012, 21:07
si
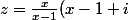)
alors
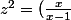^2 (x-1+i)^2=(\frac{x}{x-1})^2 (x-1+i)(x-1+i) =(\frac{x}{x-1})^2)
(........)
-
Noisetteham
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Mai 2012, 12:38
-
 par Noisetteham » 01 Oct 2012, 16:26
par Noisetteham » 01 Oct 2012, 16:26
ptitnoir a écrit:si
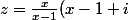)
alors
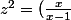^2 (x-1+i)^2=(\frac{x}{x-1})^2 (x-1+i)(x-1+i) =(\frac{x}{x-1})^2)
(........)
Merci à vous deux pour votre aide, j'ai finalement abouti et compris, encore merci :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
