Petit exercice nombres complexes
25 messages
- Page 1 sur 2 - 1, 2
Petit exercice nombres complexes
Bonjour, je rencontre des difficultés sur cet exercice:
Le plan est rapporté à un repère orthonormé direct (O;u;v)
Soit (C) la courbe représentative de la fonction f définie sur R-{1} par f(x)=x/x-1
Au point M d'affixe z, on associe le point M' d'affixe Z=z²-2(1+i)z
Démontrer que si M est un point de (C), alors M' est un point de l'axe des abscisses
Je ne comprends pas le sens de la démonstration :hein: Pouvez-vous m'aider s'il vous plait?
Merci d'avance, bonne journée.
Le plan est rapporté à un repère orthonormé direct (O;u;v)
Soit (C) la courbe représentative de la fonction f définie sur R-{1} par f(x)=x/x-1
Au point M d'affixe z, on associe le point M' d'affixe Z=z²-2(1+i)z
Démontrer que si M est un point de (C), alors M' est un point de l'axe des abscisses
Je ne comprends pas le sens de la démonstration :hein: Pouvez-vous m'aider s'il vous plait?
Merci d'avance, bonne journée.
Noisetteham a écrit:Bonjour, je rencontre des difficultés sur cet exercice:
Le plan est rapporté à un repère orthonormé direct (O;u;v)
Soit (C) la courbe représentative de la fonction f définie sur R-{1} par f(x)=x/x-1
Au point M d'affixe z, on associe le point M' d'affixe Z=z²-2(1+i)z
Démontrer que si M est un point de (C), alors M' est un point de l'axe des abscisses
Je ne comprends pas le sens de la démonstration :hein: Pouvez-vous m'aider s'il vous plait?
Merci d'avance, bonne journée.
Salut,
J'aime bien cet exo. Il faut démontrer que si l'affixe z de M satisfait f, alors M' est réel.
ptitnoir a écrit:@Noisetteham
Piste de Travail
Utilise la propriété : le nombre complexe Z est un réel si et seulement si
Cet exercice consiste donc à montrer que
Pour facilité les calculs , on a, et je te conseille d'utiliser
De plus commeon a
Mais je dois aboutir à quoi à la fin, c'est ça que je ne comprends pas :/
Attention à ne pas confonde petit z et GRAND ZNoisetteham a écrit:Donc sachant que z=x+i(x/(x-1)) je calcule Z puis Zbarre, ensuite Z-Zbarre et je dois trouver 0 ?
avec
Je t'aide en te montrant le calcul de la contraposée de petit z
Je te donne également le début des calculs à faire
Comme
on a
ptitnoir a écrit:Attention à ne pas confonde petit z et GRAND Z
, qui peut s'écrire aussi
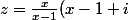)
avecun nombre réel donné différent de 1
Je t'aide en te montrant le calcul de la contraposée de petit z
Je te donne également le début des calculs à faire
Comme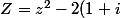 z)
on a
Donc maintenant je calcule Z en fonction de z puis Zbarre en fonction de zbarre?
CalculeNoisetteham a écrit:Donc maintenant je calcule Z en fonction de z puis Zbarre en fonction de zbarre?
en remplacant dans cette expression petit
ps)
il faut connaitre les règles sur la contraposée d'une somme de 2 complexes et la contraposée d'un produit de 2 complexes
et également que
A toi de travailler
ptitnoir a écrit:Calcule
en remplacant dans cette expression petitet petit
par leur valeur en fonction de
(qui est un réel)
ps)
il faut connaitre les règles sur la contraposée d'une somme de 2 complexes et la contraposée d'un produit de 2 complexes
et également que( avec x et y 2 réels donnés)
A toi de travailler
est-ce normal que j'ai des calculs énormes par exemple j'ai Z=[(x/(x-1))(x-1+i)]² -2[(x/(x-1))(x-1+i)] -2 [(x/(x-1))(x-1+i)]i ?
Bonjour,
pour ma part, je ne me serai pas embrouillée avec les z barre.
Tu sais que M appartient à C, donc les coordonnées de M vérifient l'équation de C, soit
M(x, x/x-1).
Donc z=x+i(x/x-1)
Ensuite, tu calcules z² et tu remplaces tout ça dans Z=z²-2(1+i)z.
En principe, si M' appartient à l'axe de x, tu dois trouver un résultat réel, c'est-à-dire que la partie imaginaire est nulle(il n'y a plus de i dans ton équation).
Et oui, pour répondre à ta question, les calculs sont un peu longs, mais avec de la méthode, tu arriveras au bout.
pour ma part, je ne me serai pas embrouillée avec les z barre.
Tu sais que M appartient à C, donc les coordonnées de M vérifient l'équation de C, soit
M(x, x/x-1).
Donc z=x+i(x/x-1)
Ensuite, tu calcules z² et tu remplaces tout ça dans Z=z²-2(1+i)z.
En principe, si M' appartient à l'axe de x, tu dois trouver un résultat réel, c'est-à-dire que la partie imaginaire est nulle(il n'y a plus de i dans ton équation).
Et oui, pour répondre à ta question, les calculs sont un peu longs, mais avec de la méthode, tu arriveras au bout.
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
