Coordonnée d'un point d'intersection entre deux foncions?
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 26 Sep 2012, 09:26
par Anonyme » 26 Sep 2012, 09:26
yam33 a écrit:C'est une déduction puisque A est un point de la courbe.
OUI A appartient à la courbe et la question est : cette courbe est elle un arc de cercle ?
donc ta déduction ne veut rien dire....
Fais un dessin ( en prenant par exemple 4 carreaux pour un unité sur les 2 axes ) et mesure avec ta règle OA
-
yam33
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Sep 2012, 20:41
-
 par yam33 » 26 Sep 2012, 09:31
par yam33 » 26 Sep 2012, 09:31
OA n'est pas égale à OJ et OA. Car OA est le rayon.
-
yam33
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Sep 2012, 20:41
-
 par yam33 » 26 Sep 2012, 09:33
par yam33 » 26 Sep 2012, 09:33
Donc il faut calculer OA, pour ensuite démontrer que c'est un arc de cercle?
-
yam33
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Sep 2012, 20:41
-
 par yam33 » 26 Sep 2012, 09:36
par yam33 » 26 Sep 2012, 09:36
OA est donc le rayon puisque A appartient à la courbe. Et OJ=OI=1. Le diamètre est égal à 2.
-
yam33
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Sep 2012, 20:41
-
 par yam33 » 26 Sep 2012, 09:37
par yam33 » 26 Sep 2012, 09:37
[quote="yam33"]OA est donc le rayon puisque A appartient à la courbe. Et OJ=OI=1.
-
yam33
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Sep 2012, 20:41
-
 par yam33 » 26 Sep 2012, 09:38
par yam33 » 26 Sep 2012, 09:38
OA est donc le rayon puisque A appartient à la courbe. Et OJ=OI=1.
-
Anonyme
 par Anonyme » 26 Sep 2012, 09:38
par Anonyme » 26 Sep 2012, 09:38
Si la courbe de g est un arc de cercle de centre O alors OI et OJ et OA sont des rayonsEn classe de seconde tu as du apprendre (chapitre vecteur)
si les coordonnées du point A sont
)
si les coordonnées du point B sont
)
dans un repère
)
orthornormé
Alors on a la formule
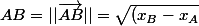^2 +(y_B -y_A)^2})
ps)
calcule OA avec cette formule
-
yam33
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Sep 2012, 20:41
-
 par yam33 » 26 Sep 2012, 09:39
par yam33 » 26 Sep 2012, 09:39
J'ai fait une connerie dans le post. Le diamètre n'est pas égal à 2.
-
yam33
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Sep 2012, 20:41
-
 par yam33 » 26 Sep 2012, 09:42
par yam33 » 26 Sep 2012, 09:42
Oui je connait cette formule c'est juste que je l'ai mal utilisé. Donc OA= 9/8
-
Anonyme
 par Anonyme » 26 Sep 2012, 09:46
par Anonyme » 26 Sep 2012, 09:46
yam33 a écrit:Oui je connait cette formule c'est juste que je l'ai mal utilisé. Donc OA= 9/8
non , refais ton calcul de OA moins vite avec la formule du post précédent
puis compare OA avec OI et OJ
-
yam33
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Sep 2012, 20:41
-
 par yam33 » 26 Sep 2012, 09:50
par yam33 » 26 Sep 2012, 09:50
Je trouve OA= 1.125 soit 9/8. Je retrouve la même chose. O(0;0;) et A(3/4;3/4) OA= racine(3/4-0)²+(3/4-0)².
-
Anonyme
 par Anonyme » 26 Sep 2012, 09:54
par Anonyme » 26 Sep 2012, 09:54
yam33 a écrit:Je trouve OA= 1.125 soit 9/8.
Je ne trouve pas ce résultat mais peu importe
Comme

l'arc de cercle de centre O et de rayon 1 qui passe par les 2 points I et J ne passe pas par le point A
Donc tu peux conclure ton exercice
A+

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 26 Sep 2012, 10:28
par chan79 » 26 Sep 2012, 10:28
ptitnoir a écrit:Pourquoi puisque la fonction carré est une bijection sur R+ ?
C'est parce que, quand on élève au carré , on ne raisonne pas par équivalence
Si on avait trouvé x=5 il aurait fallu l'éliminer car la racine de (1-5) n'existe pas
-
Anonyme
 par Anonyme » 26 Sep 2012, 10:45
par Anonyme » 26 Sep 2012, 10:45
chan79 a écrit:C'est parce que, quand on élève au carré , on ne raisonne pas par équivalence
Si on avait trouvé x=5 il aurait fallu l'éliminer car la racine de (1-5) n'existe pas
On peut raisonner par équivalence car on est sur R+
Il aurait fallu vérifier que la solution trouvée appartient au domaine de définition
Remarque :
On ne peut écrire
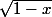
uniquement si
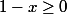
et on a bien

-
yam33
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Sep 2012, 20:41
-
 par yam33 » 26 Sep 2012, 11:02
par yam33 » 26 Sep 2012, 11:02
Donc ce n'est pas un arc de cercle. A ce sujet comment fait on pour déterminer l'expression d'une parabole par lecture graphique uniquement?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 26 Sep 2012, 11:05
par chan79 » 26 Sep 2012, 11:05
ptitnoir a écrit:On peut raisonner par équivalence car on est sur R+
Il aurait fallu vérifier que la solution trouvée appartient au domaine de définition
Remarque :
On ne peut écrire
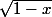
uniquement si
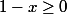
et on a bien

on est d'accord dans ce cas là si on vérifie ensuite pour le domaine de définition
J'aurais tendance à conseiller aux élèves de vérifier, surtout quand la solution est simple même s'il n'y a pas à le rédiger obligatoirement
-
Anonyme
 par Anonyme » 26 Sep 2012, 11:16
par Anonyme » 26 Sep 2012, 11:16
chan79 a écrit:on est d'accord dans ce cas là si on vérifie ensuite pour le domaine de définition
J'aurais tendance à conseiller aux élèves de vérifier, surtout quand la solution est simple même s'il n'y a pas à le rédiger obligatoirement
OUI MAIS c'est aussi important de présenter les choses dans l'ordre....
Et c'est vrai que les équivalences sont souvent employées par les élèves à tord et à travers....
et qu'il vaut mieux ne pas trop en parler...
Je pense que tu veux parler de la vérification des calculs et du calcul de g(3/4) (à la calculatrice) qui permet de vérifier les calculs qui ont été faits
-
yam33
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Sep 2012, 20:41
-
 par yam33 » 26 Sep 2012, 11:28
par yam33 » 26 Sep 2012, 11:28
Auriez vous une piste: je connait les deux racines x1 et x2 et le sommet de coordonnées S et la parabole est toujours positives tournée vers le bas donc avec a<0 dans le cas d'un trinôme. J'ai pu avoir la forme canonique mais il me manque a.
Merci
-
Anonyme
 par Anonyme » 26 Sep 2012, 11:31
par Anonyme » 26 Sep 2012, 11:31
S a pour coordonnées (-b/2a , f(-b/2a))
-
yam33
- Membre Naturel
- Messages: 65
- Enregistré le: 25 Sep 2012, 20:41
-
 par yam33 » 26 Sep 2012, 11:48
par yam33 » 26 Sep 2012, 11:48
Je développe la forme canonique puis je calcule (a) en utilisant la formule du sommet.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
