Variation d'une fonction à valeur absolue.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
 par DamagedBrain » 09 Sep 2012, 13:31
par DamagedBrain » 09 Sep 2012, 13:31
Bonjour,
J'ai un DM à rendre pour jeudi, cependant, après des heures de recherches, je n'ai toujours rien trouvé. :doh:
Il nous faut trouver les variations de la fonction
=abs(x^2-4x-9))
. Quelqu'un pourrait-il m'aider, ou au moins m'orienter sur la marche à suivre ?
Merci d'avance.
Camille.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 09 Sep 2012, 13:34
par Kikoo <3 Bieber » 09 Sep 2012, 13:34
Yo,
Pour trouver les variations d'une fonction, tu dérives dans la plupart des cas. Ici, je t'encourage à le faire, c'est plus court.
Mais la valeur absolue gène, et il te faut l'enlever, en distinguant deux cas :
si on a g(x)=|f(x)|, alors g(x) vaut ***** quand f(x) est positif et vaut ***** quand f(x) est négatif.
Comment savoir quand f est positive ou négative ? A toi de voir.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 13:38
par Luc » 09 Sep 2012, 13:38
Salut,
pour t'aider, définis une fonction auxiliaire g par
=x^2-4x-9)
. g est une fonction polynomiale dont tu peux calculer les racines, et donc déterminer le signe et le sens de variation en fonction de x. Ensuite, utilises le fait que f(x)=+g(x) là ou g est positive et f(x)=-g(x) là ou g est négative.
Edit: grillé :we:
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 09 Sep 2012, 13:41
par Kikoo <3 Bieber » 09 Sep 2012, 13:41
Vas y, Luc, je vais travailler !
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 13:42
par Luc » 09 Sep 2012, 13:42
Kikoo <3 Bieber a écrit:Vas y, Luc, je vais travailler !
ok! bon travail!
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 09 Sep 2012, 13:43
par Kikoo <3 Bieber » 09 Sep 2012, 13:43
Hehe ^^ De toute façon je risque bien de reposter dans quelques minutes dans le sous-forum chimie.
Grrrr... la chimie :lol:
 par DamagedBrain » 09 Sep 2012, 13:55
par DamagedBrain » 09 Sep 2012, 13:55
Merci de votre aide.
Et bien, je sais que g(x) est décroissante de -infini à 2 (et descend jusqu'à -13) et est à nouveau croissante de 2 à +infini. Après en ce qui concerne le reste, j'avoue ne pas avoir bien compris...
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 14:01
par Luc » 09 Sep 2012, 14:01
DamagedBrain a écrit:Merci de votre aide.
Et bien, je sais que g(x) est décroissante de -infini à 2 (et descend jusqu'à -13) et est à nouveau croissante de 2 à +infini. Après en ce qui concerne le reste, j'avoue ne pas avoir bien compris...
Ok. Tu sais également résoudre léquation g(x)=0, dont je note les racines
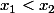
. Du coup tu connais le signe de g(x), donc la valeur de f(x) en fonction de la valeur de x. Regarde séparément les intervalles ]- l'infini,

], [

,2], [2,

], [

, + l'infini[ .
 par DamagedBrain » 09 Sep 2012, 14:23
par DamagedBrain » 09 Sep 2012, 14:23

?
Donc f(x) est décroissant sur

, croissant sur

, décroissant sur

et croissant sur

?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 14:38
par Luc » 09 Sep 2012, 14:38
DamagedBrain a écrit:
?
Donc f(x) est décroissant sur

, croissant sur

, décroissant sur

et croissant sur

?
Oui c'est bon. Pour simplifier lécriture, remarque que

.
 par DamagedBrain » 09 Sep 2012, 14:40
par DamagedBrain » 09 Sep 2012, 14:40
Très bien, merci beaucoup pour votre aide :)
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 09 Sep 2012, 14:44
par Luc » 09 Sep 2012, 14:44
DamagedBrain a écrit:Très bien, merci beaucoup pour votre aide

Nhésite pas a repasser si tu bloques sur un exo

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités