Division

par **khaoua2** » 04 Juil 2006, 23:56

Bonjour,

Quel est le plus petit nombre qui, divisé par 2,3,4,5,6, donne respectivement les restes 1,2,3,4,5, ??

j'ai essayé de faire une equation tel A est le nombre voulu
x2+1=A
(x)3 + 2=A
. .
. .
. .

Ca ne donne pas le meme nombre A.

merci mille fois pour l'aide
a bientot.

par **BancH** » 05 Juil 2006, 00:24

Déjà, tes équations sont fausses, tu n'as pas une seule inconnue mais

.

,

... ou alors

,

Mais tu ne peux pas résoudre le problème par combinaisons linéaires je pense.

par **Sdec25** » 05 Juil 2006, 00:46

Moi j'avais lu "divisé successivement", donc j'ai cherché et j'ai trouvé 1439. Pour rien :briques: :ptdr:

par **BancH** » 05 Juil 2006, 00:50

Tu veux dire que tu as confondu avec " A divisé par 2,6,24,120,720 donne respectivement 1,2,3,4,5 " ?

par **Sdec25** » 05 Juil 2006, 00:52

Non j'ai cru divisé par 2 puis par 3 puis par 4... donne comme reste 1 puis 2 puis 3...

par **BancH** » 05 Juil 2006, 00:57

T'es sûr pour 1319 ?

par **BancH** » 05 Juil 2006, 01:00

Sdec25 a écrit:Moi j'avais lu "divisé successivement", donc j'ai cherché et j'ai trouvé 1319. Pour rien :briques: :ptdr:

Ton résultat est bon mais ce n'est pas le plus petit nombre.

par **Sdec25** » 05 Juil 2006, 01:01

Vi j'en étais pas trop sûr.
Comment tu as fait pour trouver qu'il y a plus petit ?

par **BancH** » 05 Juil 2006, 01:04

C'est parce que la réponse trouvée par Rain' : 59, est correcte et 59<1319.

par **Sdec25** » 05 Juil 2006, 01:16

Je rectifie : le nombre que j'ai trouvé est 719 pas 1319.
Mais ce n'est pas ce qui était demandé donc ce nombre n'est pas la solution.

par **aviateurpilot** » 05 Juil 2006, 02:09

Quel est le plus petit nombre qui, divisé par 2,3,4,5,6, donne respectivement les restes 1,2,3,4,5, ??

soit n ce nombre

n+1 divisible par 2,3,4,5, et 6
n+1 divisible par

donc le plus petit n est

:zen:

par **Patastronch** » 05 Juil 2006, 02:42

aviateurpilot a écrit:soit n ce nombre

n+1 divisible par 2,3,4,5, et 6
n+1 divisible par
donc le plus petit n est
:zen:

29/4 il reste ??? ok, donc c'est faux.

MAis ty etais presque ton erreur rectifiée :

n+1 divisible par

donc le plus petit n est

par **aviateurpilot** » 05 Juil 2006, 02:54

j'ai dit n+1 divisible par 2,3,4,5, et 6
j'ai juste oublié de multiplier 30 par 2 pour qu'il soit divisible par 4
merci pour cette petite remarque Patastronch.
2eme methode:(pour pour ceux qui ne connaisent pas la congruence
si on divise un nombre par

est on trouve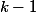

comme rest alors il lui faut 1 pour qu'il soit divisible par k
=>si n est le plus petit nombre qui, divisé par 2,3,4,5,6, donne respectivement les restes 1,2,3,4,5,
=> alors n+1 est le plus petit nombre qui, divisé par 2,3,4,5,6, donne respectivement les restes 0,0,0,0,0
=>donc n+1 est le plus nombre divisible par 2,3,4,5,6
=> n+1 est le plus petit nombre divisible par 3 , 5 et 2:2fois
par suite

n=59

par **khaoua2** » 05 Juil 2006, 14:00

bonjour

comment avez-vous trouver la solution :

n+1 = 2* 3* 5=60
merci

par **aviateurpilot** » 05 Juil 2006, 14:42

n+1 est divisible par 2,3,4,5 et 6
on cherche la valeur minimal de n+1
c'est

par **khaoua2** » 05 Juil 2006, 14:44

Ppcm.????????????????? 60,,???

par **Sdec25** » 05 Juil 2006, 14:50

Le reste de n par 2 est 1 donc n+1 est multiple de 2
Le reste de n par 3 est 2 donc n+1 est multiple de 3
etc

n+1 est multiple de 2, 3, 4, 5 et 6 donc le plus petit n+1 qu'on puisse trouver est le plus petit multiple de 2, 3, 4, 5 et 6 (PPCM = plus petit commun multiple).

par **khaoua2** » 05 Juil 2006, 15:44

merci
j(ai compris maintenant.

par **aviateurpilot** » 05 Juil 2006, 16:04

moi a écrit:=>si n est le plus petit nombre qui, divisé par 2,3,4,5,6, donne respectivement les restes 1,2,3,4,5,
=> alors n+1 est le plus petit nombre qui, divisé par 2,3,4,5,6, donne respectivement les restes 0,0,0,0,0

Sdec25 a écrit:Le reste de n par 2 est 1 donc n+1 est multiple de 2
Le reste de n par 3 est 2 donc n+1 est multiple de 3
etc

n+1 est multiple de 2, 3, 4, 5 et 6 donc le plus petit n+1 qu'on puisse trouver est le plus petit multiple de 2, 3, 4, 5 et 6 (PPCM = plus petit commun multiple).

il n'a fait que repeter ce que j'ai dit en modifiant la forme des phrases
je ne sais pas pour quoi tu n'as pas compris ce que j'ai dit :hein:

par **flight** » 05 Juil 2006, 20:03

salut à tous , aviateur pilot etait bien partit , sa synthèse par les congruences est pas mal , justement on pourrait remarquer d'apres une ecriture tout simple que :
N=2q1+2-1
N=3q2+3-1

N=6q5+6-1

il vient alors N+1 multiple commun de (2,3,...,6) soit 60k avec k appartenant à IN,

soit N+1=k.ppcm(2,3,...,6)=60k et N=60k-1 le plus petit entier N pourra etre obtenu en prenant k=1

soit N=60-1=59

Division

division

re

Re

Qui est en ligne