Somme

[Skullkid]

Ouais tan^(-1) est aussi utilisée comme notation pour cotan, mais c'est vrai que c'est préférable de n'utiliser que les notations univoques sans exposant. Pour la 2 ça ne va toujours pas, rho est à la puissance k dans la somme, pas à la puissance n-1. Ne cherche pas à calculer trop loin, applique la formule donnant la somme des termes d'une suite géométrique, ça suffit.

[Kikoo <3 Bieber]

D'accord !

J'y reviens :
Ok, mais à partir d'ici, ne faut-il pas que je trouve une expression plus simple pour la question suivante ?

[Skullkid]

Non, enfin tu n'as pas besoin d'introduire rhô et x : . Cette forme suffit amplement à répondre à la question suivante.

[Kikoo <3 Bieber]

Ok,
On en arrive à déterminer les racines n-ièmes de l'unité : , non ? Mais il y aurait alors exactement n racines... :/

[Skullkid]

C'est là qu'il faut faire attention aux équivalences. n'est pas équivalent à mais à . Le plus simple étant de procéder par implication puis réciproque : si alors z est une des n racines n-ièmes de l'unité. Réciproquement, toutes les racines conviennent, sauf 1.

[Kikoo <3 Bieber]

Oui, tout à fait ! J'avais oublié d'omettre le 1...
Donc j'ai mes solutions : .
Pour le 4), je fais la somme des racines :
si je me trompe pas !


Edit : dans ma précipitation, j'ai oublié qu'il fallait toujours remplacer z ! Je corrige.

Correction : les n-1 solutions sont de la forme , pour k entier compris entre 1 et n-1

Après, il est certain que c'est plus dur de sommer :mur:

[Skullkid]

Tu vas trop vite et tu t'embrouilles. Fais les choses calmement et arrête de t'accrocher à ce x qui n'est introduit nulle part.

Quelles sont les n-1 solutions de ? Il n'y a pas de x dans cette équation ni dans l'énoncé donc si tu veux utiliser un x il faut le définir.

[Kikoo <3 Bieber]

Salut,

Le x est un argument de z non ? Je ne vois pas :triste:

[Skullkid]

Salut,

Le x est un argument de z non ? Je ne vois pas :triste:

Qui est z ? On te demande les solutions de l'équation d'inconnue u. Les seules lettres qui apparaissent dans cette équation sont k, n, u et i. Pas de x, pas de z.

C'est comme si je te demandais de résoudre u² +7u - 1 = 0 et que tu me répondais que la solution est u = 3x + 4. Tu comprends pourquoi ça ne va pas ?

[Kikoo <3 Bieber]

D'accord, je vais essayer de faire simple ! ^^

La somme vaut
Nous en arrivons à poser
Résoudre S=0 revient à résoudre , soit 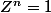, avec .
Nous posons de nouveau avec le module de Z et un de ses arguments. Nous constatons que vaut 1 et que .
Nous trouvons que les solutions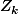 au nombre de n-1 de cette équation valent .
En nous servant de la question un, on trouve que les solutions finales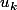 au nombre de n-1 valent .

J'ai bien défini les variables ici ! Enfin j'espère !

[Skullkid]

Tu es têtu, je t'ai dit qu'il fallait arrêter de t'accrocher à l'introduction d'un argument. Dans ta rédaction, phi dépend de Z qui dépend de l'inconnue u donc tu as exprimé u en fonction de u, ce qui n'a pas vraiment de sens. Tu es trop occupé à introduire de nouvelles lettres qui t'encombrent inutilement et du coup tu fais des fautes d'inattention.

Relis ton post avec attention et essaye de voir l'erreur. Et arrête de chercher à rajouter des lettres, il y en a suffisamment comme ça.

[Kikoo <3 Bieber]

Tout à fait, je ne vois plus le fond du problème, et je ne discerne pas la voie à laquelle tu me mènes... J'en suis navré :(
J'essaierai d'y réfléchir encore dans la journée.
En tout cas, merci encore pour ton soutien et ton aide ! Je t'avoue que je suis lassé de cet exercice : il faudra bien que je le finisse !

[Skullkid]

Désolé je viens seulement de me remémorer ce topic. Voici un exemple de rédaction pour la solution :

3 - Puisque n'est jamais égal à 1 lorsque u parcourt C\{i}, d'après la réponse à la question 2, pour tout complexe u distinct de i : . Cette quantité est nulle si et seulement si , c'est-à-dire si est une racine n-ième de l'unité. On est donc amené à résoudre pour chaque k dans |[1,n]|. D'après la réponse à la question 1, il y a une solution si et seulement si k appartient à |[1,n-1]|, à savoir .

4 - donc .

[Kikoo <3 Bieber]

D'accord, donc le problème pour la question 3 était définitivement un problème de rédaction ^^
Je ne savais pas comment faire pour ne pas introduire un nouveau complexe avec x et blabla...
En tout cas, c'est clair comme de l'eau de roche, merci !

Pour la 4), j'aurais pas vu l'astuce ! :o

[Skullkid]

Pour la 4, tester ce que ça donne pour les premières valeurs de n fait apparaître les termes qui s'annulent deux à deux.