Application "tirer en arrière"

[barbu23]

Bonsoir,

J'ai du mal à comprendre la définition suivante :
Soit et deux -espaces vectoriels et une application linéaire, on définit par :

Je voudrais savoir comment on note l'expression de l'application . Est-ce que c'est : ou bien ?

Merci d'avance.

[bruce.ml]

Deja il manque la definition du m. On ne sait pas d'ou il sort.
Je dirais qu'il faut definir phi par


Mais je ne suis pas bien sûr de comprendre la question.

[wserdx]

Je pense que cette définition est à rapprocher de celle d'espace dual.
Si est linéaire de dans ,
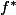
alors prend en argument une forme multilinéaire sur , et retourne une forme multilinéaire sur , .

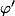
est défini par

où
Le changement de notation permet de voir qui vit dans quoi...

[bruce.ml]

Je pense que cette définition est à rapprocher de celle d'espace dual.
Si est linéaire de dans ,
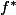
alors prend en argument une forme multilinéaire sur , et retourne une forme multilinéaire sur , .

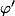
est défini par

où
Le changement de notation permet de voir qui vit dans quoi...

J'aime ta reponse. Mais je pense que le plus important est d'écrire a quels ensembles appartiennent les elements que tu utilises. Dans l'enonce du sujet, rien n'est defini, j'ai mis du temps a realiser a quels ensembles appartiennent les phis et x et m que tu utilises. Ecris tout, ça t'aidera.