Orthogonal

par **zork** » 23 Juil 2012, 13:23

bonjour,

j'ai E=

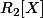
et j'ai un produit scalaire f(P,Q)

On me demande de chercher l'orthogonal de F=Vect{1,X}

Comment faire? je sais faire quand ce sont des vecteur mais avec des polynômes qu'est ce qui change?

Puis comment fais-t-on pour trouver la projection orthogonal de X² sur F?

je sais que p(X²)=a+bX avec a et b à déterminer:
du coup j'aurai calculer les produit scalaire suivant: f(X²-p(X²),1)=0 et f(X²-p(X²),X)=0 pour trouver a et b

merci

par **vincentroumezy** » 23 Juil 2012, 13:26

Salut. Si tu sais faire avec des vecteurs, tu sais aussi faire avec des polynômes, car ce sont des vecteurs de

.
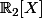
C'est quoi l'expression de ton produit scalaire ?

par **zork** » 23 Juil 2012, 14:04

par **egan** » 23 Juil 2012, 15:17

Ya pas un - dans l'exponentiel ?

par **vincentroumezy** » 23 Juil 2012, 18:05

Je pense aussi (le racine de Pi rappelle l'intégrale de Gauss !)

par **zork** » 23 Juil 2012, 19:16

si il y a un -

par **vincentroumezy** » 23 Juil 2012, 19:20

Bon.
Pour trouver l'orthogonal de F, il faut trouver tous les polynômes P de degré au plus 2 tels que f(P,a+bX)=0.

par **zork** » 23 Juil 2012, 19:27

d'accord et pour la projection orthogonale de X² sur F

par **vincentroumezy** » 23 Juil 2012, 19:30

Ton raisonnement du premier message à l'air bon.

par **sabaga** » 23 Juil 2012, 19:32

bonjour.
tu peux utélisér méthode de Gram-schmidt

par **zork** » 23 Juil 2012, 19:38

mais pourquoi X²-p(X²) et pas p(X²)-X²?

par **vincentroumezy** » 23 Juil 2012, 19:41

Si ça fait 0 avec X²-p(X²), pareil avec l'opposé (vu que le produit scalaire est une forme bilinéaire).

par **zork** » 23 Juil 2012, 19:50

j'aurais encore une question:

pour chercher l'orthogonal de F tu m'as conseillé de chercher les polynômes P tel que f(P,a+bX)

mais dans les question précédentes j'ai trouver la matrice du produit scalaire dans la base canonique {1,X,X²}
N'est il pas possible d'utiliser cette matrice comme avec les vecteurs quand on cherche l'orthogonal?

par **sabaga** » 23 Juil 2012, 20:47

par **sabaga** » 23 Juil 2012, 20:56

je vous propose un éxemple(gram-schmidt)

par **vincentroumezy** » 24 Juil 2012, 08:24

zork a écrit:j'aurais encore une question:

pour chercher l'orthogonal de F tu m'as conseillé de chercher les polynômes P tel que f(P,a+bX)

mais dans les question précédentes j'ai trouver la matrice du produit scalaire dans la base canonique {1,X,X²}
N'est il pas possible d'utiliser cette matrice comme avec les vecteurs quand on cherche l'orthogonal?

Quelle est ta matrice, et comment mettrais tu le produit scalaire sous forme "vectorielle" ?

Orthogonal

orthogonal

Qui est en ligne