Conique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
hanabi
- Messages: 4
- Enregistré le: 29 Mai 2012, 19:48
-
 par hanabi » 29 Mai 2012, 19:54
par hanabi » 29 Mai 2012, 19:54
Bonjour,
pouvez-vous m'aider à déterminer les caractéristiques de C: x²+ 4y²+ 4x+8y=0
Merci :lol3:
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 29 Mai 2012, 19:59
par globule rouge » 29 Mai 2012, 19:59
hanabi a écrit:Bonjour,
pouvez-vous m'aider à déterminer les caractéristiques de C: x²+ 4y²+ 4x+8y=0
Merci :lol3:
Salut :salut:

Il s'agit simplement d'un cercle !
Julie

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 29 Mai 2012, 20:03
par chan79 » 29 Mai 2012, 20:03
globule rouge a écrit:Salut :salut:

Il s'agit simplement d'un cercle !
Julie
Salut
Une ellipse, je dirais
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 29 Mai 2012, 20:05
par globule rouge » 29 Mai 2012, 20:05
En effet, mais un cercle n'est-il pas un cas particulier d'ellipse ? :)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 29 Mai 2012, 20:24
par chan79 » 29 Mai 2012, 20:24
globule rouge a écrit:En effet, mais un cercle n'est-il pas un cas particulier d'ellipse ?

oui, mais cette ellipse n'est pas un cercle

-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 29 Mai 2012, 20:42
par globule rouge » 29 Mai 2012, 20:42
chan79 a écrit:oui, mais cette ellipse n'est pas un cercle

Ah bon ??

-
hammana
- Membre Relatif
- Messages: 477
- Enregistré le: 24 Avr 2012, 20:26
-
 par hammana » 29 Mai 2012, 21:11
par hammana » 29 Mai 2012, 21:11
hanabi a écrit:Bonjour,
pouvez-vous m'aider à déterminer les caractéristiques de C: x²+ 4y²+ 4x+8y=0
Merci :lol3:
Comme il n'ya pas de terme en xy, il s'agit d'une ellipse dont les axes sont parallèles à Ox et Oy.
L'équation de C peut s'écrire
^2 +4(y+1)^2=8)
En faisant une translation des axes et appelant X, Y les nouvlles coordonnées tu peux écrire l'équation canonique de l'ellipse (je suppose que tu connais)
X*2/8+Y*2/2=1
Je te laisse trouver le centre, le grand axe, le petit axe, et la représentation graphique de l'ellipse
(j'expère n'avoir pas fait d'erreurs)
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 29 Mai 2012, 21:18
par globule rouge » 29 Mai 2012, 21:18
Ah oui, je vois où j'ai pu faire des confusions :( Excusez-moi d'avoir parlé trop vite !
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Mai 2012, 05:40
par Dinozzo13 » 30 Mai 2012, 05:40
Salut !
globule rouge a écrit:Salut :salut:

Il s'agit simplement d'un cercle !
Julie
Un cercle à pour équation cartésienne
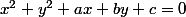
:+++:
Tu remarqueras que les coefficients devant

et
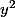
doivent être égaux :++:
-
Dlzlogic
- Membre Transcendant
- Messages: 5273
- Enregistré le: 14 Avr 2009, 12:39
-
 par Dlzlogic » 30 Mai 2012, 10:45
par Dlzlogic » 30 Mai 2012, 10:45
Bonjour,
Je vais essayer de défendre un peu globule rouge, on peut dire que c'est un cercle un peu (très) aplati, ou un cercle qu'on regarde de travers ou de haut, ou un cercle qu'on a transformé par affinité.
De toute façon, c'est pas une hyperbole.
-
hanabi
- Messages: 4
- Enregistré le: 29 Mai 2012, 19:48
-
 par hanabi » 30 Mai 2012, 14:50
par hanabi » 30 Mai 2012, 14:50
hammana a écrit:Comme il n'ya pas de terme en xy, il s'agit d'une ellipse dont les axes sont parallèles à Ox et Oy.
L'équation de C peut s'écrire
^2 +4(y+1)^2=8)
En faisant une translation des axes et appelant X, Y les nouvlles coordonnées tu peux écrire l'équation canonique de l'ellipse (je suppose que tu connais)
X*2/8+Y*2/2=1
Je te laisse trouver le centre, le grand axe, le petit axe, et la représentation graphique de l'ellipse
(j'expère n'avoir pas fait d'erreurs)
Re-bonjour, et merci.
C'est donc une ellipse d'équation x²/8+ y²/2=1.
Ses caractéristiques sont:
centre: (-2,1)
axes: x= -2 et y=1
sommets: (2;)2-2; 1) (-2;)2-2; 1) (-2;

2 +1 ) (-2; -;)2+1 )
foyers: (±

6-2; 1)
e: (;)3)
D: x=-2 ±8/;)6
Est-ce correct?
-
hammana
- Membre Relatif
- Messages: 477
- Enregistré le: 24 Avr 2012, 20:26
-
 par hammana » 01 Juin 2012, 11:00
par hammana » 01 Juin 2012, 11:00
hanabi a écrit:Re-bonjour, et merci.
C'est donc une ellipse d'équation x²/8+ y²/2=1.
Ses caractéristiques sont:
centre: (-2,1)
axes: x= -2 et y=1
sommets: (2;)2-2; 1) (-2;)2-2; 1) (-2;

2 +1 ) (-2; -;)2+1 )
foyers: (±

6-2; 1)
e: (;)3)
D: x=-2 ±8/;)6
Est-ce correct?
Les coordonnées du centre sont -2 et -1 (au lieu de -2 et 1), une erreur d'inattention sans doute ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
2 +1 ) (-2; -;)2+1 )
6-2; 1)
