étude fonction log
22 messages
- Page 1 sur 2 - 1, 2
étude fonction log
Bonsoir
En fait j'au du mal avec cette étude de fonction pourriez vous m'aider svp?
On définit la fonction k par k(x)= x log indice 3(x)
1/Définir l'ensemble de déf de k
2/Etudier les variations de k et ses lim en -00 et +00
J'ai du mal avec ce log en fait
merci d'avance de votre aide:)
En fait j'au du mal avec cette étude de fonction pourriez vous m'aider svp?
On définit la fonction k par k(x)= x log indice 3(x)
1/Définir l'ensemble de déf de k
2/Etudier les variations de k et ses lim en -00 et +00
J'ai du mal avec ce log en fait
merci d'avance de votre aide:)
Salut !
En premier lieu, il faut savoir que :
Pour tout et pour tout
et pour tout  :
: =\frac{\ln x}{ln a}) .
.
Par conséquent :
=x \log_3(x)= \frac{x \ln x}{\ln 3}) .
.
1°) est définie si et seulement si
est définie si et seulement si  , rien de bien méchant ^^, donc
, rien de bien méchant ^^, donc 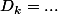 .
.
2°) Ensuite, les limites : et
et  étant des limites de références, tu déduis facilement que
étant des limites de références, tu déduis facilement que =...) et
et =...)
Pour étudier les variations de k, étudie le signe de la dérivée k' de k.
@+ :+++:
En premier lieu, il faut savoir que :
Pour tout
Par conséquent :
1°)
2°) Ensuite, les limites :
Pour étudier les variations de k, étudie le signe de la dérivée k' de k.
@+ :+++:
non justement donc je met rien en -00 car la fonction n'est pas définie
sauf que dans ton précédent post tu écrivais :
la lim en -00 vaut donc 0
effectivement, il faut écrire que n'étant pas définie pour x<0, k ne peut avoir de limite
tu es sûr que tu as bien recopié l'énoncé ? qu'il n'y a pas une valeur absolue qui traîne ?
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
