Domaine de définition fonction log et exp
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anaaaais
- Messages: 6
- Enregistré le: 30 Déc 2010, 17:07
-
 par Anaaaais » 30 Déc 2010, 17:12
par Anaaaais » 30 Déc 2010, 17:12
Bonjour :)
Pourriez vous m'aidez à trouver le domaine de déf de cette fonction :
f(x) = ln(e2x - ex +1)
Merci d'avance!
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 30 Déc 2010, 17:17
par XENSECP » 30 Déc 2010, 17:17
 = \ln{\left(e^{2x}-e^x+1\right)})
Quel est le domaine de définition du LN ?
Tu poseras

quand tu en auras besoin

-
Anaaaais
- Messages: 6
- Enregistré le: 30 Déc 2010, 17:07
-
 par Anaaaais » 30 Déc 2010, 17:19
par Anaaaais » 30 Déc 2010, 17:19
XENSECP a écrit: = \ln{\left(e^{2x}-e^x+1\right)})
Quel est le domaine de définition du LN ?
Tu poseras

quand tu en auras besoin

le domaine de dèf de ln c'est ]0;+inf[
ça sert à quoi de poser X=e^x?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 30 Déc 2010, 17:22
par Sylviel » 30 Déc 2010, 17:22
Et bien ça permet de tomber sur une fonction connue de X dont tu pourras déterminer le signe...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Anaaaais
- Messages: 6
- Enregistré le: 30 Déc 2010, 17:07
-
 par Anaaaais » 30 Déc 2010, 17:27
par Anaaaais » 30 Déc 2010, 17:27
Sylviel a écrit:Et bien ça permet de tomber sur une fonction connue de X dont tu pourras déterminer le signe...
c'est sur comme ca c'est plus logique :/........
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 30 Déc 2010, 17:29
par XENSECP » 30 Déc 2010, 17:29
Anaaaais a écrit:c'est sur comme ca c'est plus logique :/........
J'ai fait un message pour 2 étapes histoire de pas reposter toutes les 2 minutes

-
Anaaaais
- Messages: 6
- Enregistré le: 30 Déc 2010, 17:07
-
 par Anaaaais » 30 Déc 2010, 17:34
par Anaaaais » 30 Déc 2010, 17:34
XENSECP a écrit:J'ai fait un message pour 2 étapes histoire de pas reposter toutes les 2 minutes

oui mais jte jure ça m'aide pas.
e2x - ex + 1
si je pose X=ex
ça fait : X? - X + 1
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 30 Déc 2010, 17:36
par XENSECP » 30 Déc 2010, 17:36
Anaaaais a écrit:oui mais jte jure ça m'aide pas.
e2x - ex + 1
si je pose X=ex
ça fait : X? - X + 1
Ouais je sais désolé.
Oui ça fait
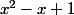
. Trinôme dont tu connais le signe normalement (à n'étudier que sur
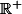
)
-
Anaaaais
- Messages: 6
- Enregistré le: 30 Déc 2010, 17:07
-
 par Anaaaais » 30 Déc 2010, 17:49
par Anaaaais » 30 Déc 2010, 17:49
x2 - x + 1 c'est dérivale sur R
Et ln : ]0;+inf[
Donc Df = ]0; =inf[
C'est ça nn?
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 30 Déc 2010, 17:55
par Billball » 30 Déc 2010, 17:55
Anaaaais a écrit:x2 - x + 1 c'est dérivale sur R
Et ln : ]0;+inf[
Donc Df = ]0; =inf[
C'est ça nn?
faut pas que ca soit dérivable, faut que ca soit positif
-
Anaaaais
- Messages: 6
- Enregistré le: 30 Déc 2010, 17:07
-
 par Anaaaais » 30 Déc 2010, 17:59
par Anaaaais » 30 Déc 2010, 17:59
ah oui fffff..
donc le domaine c'est R+ soit ]0;+inf[
Et dire q c'est la première question de mon DM :m
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 30 Déc 2010, 18:00
par Billball » 30 Déc 2010, 18:00
Anaaaais a écrit:ah oui fffff..
donc le domaine c'est R+ soit ]0;+inf[
Et dire q c'est la première question de mon DM :m
ouai c ca :lol3:
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 30 Déc 2010, 19:09
par XENSECP » 30 Déc 2010, 19:09
Billball a écrit:ouai c ca :lol3:
Non c'est pas ça !!!
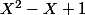
c'est strictement positif sur

donc le domaine de définition de f c'est

entier

-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 30 Déc 2010, 19:15
par Billball » 30 Déc 2010, 19:15
XENSECP a écrit:Non c'est pas ça !!!
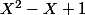
c'est strictement positif sur

donc le domaine de définition de f c'est

entier

merde oué, désolé, merci de m'avoir repris
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
