Exercices nombres complex
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 22 Jan 2011, 19:25
par tite_prune » 22 Jan 2011, 19:25
C'est la droite d'équation x=5 mais je crois pas que ça marche comme ça la rédaction avec les complexes.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 22 Jan 2011, 19:31
par Sa Majesté » 22 Jan 2011, 19:31
Si ça marche
Alors maintenant la démo géométrique
|10-z|=PM
|z|=OM
donc |10-z|=|z| équivaut à PM=OM donc l'ensemble cherché est la médiatrice de [OP]
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 22 Jan 2011, 19:41
par tite_prune » 22 Jan 2011, 19:41
a oui !! Je trouve ça mieux comme rédaction en plus ! Merci beaucoup pour votre aide.
Ensuite pour que u/z soit imaginaire pure il faut que sa partie réelle =0 donc si j'ai bien développer j'ai:
u/z=

=
}{x^2+y^2})
Pouvez vous vérifier si cela est bon avant que je comment à calculer RE(u/z)=0?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 22 Jan 2011, 20:06
par Sa Majesté » 22 Jan 2011, 20:06
Ben en fait j'ai pas trop envie de faire de gros calculs
Alors j'utiliserais plutôt la propriété : Z est imaginaire pur ssi
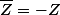
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 23 Jan 2011, 18:12
par tite_prune » 23 Jan 2011, 18:12
Donc ici on peut dire que u/z imaginaire pure

=-u/z ? Je fais le calcul et je le poste

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 18:14
par Sa Majesté » 23 Jan 2011, 18:14
tite_prune a écrit:Donc ici on peut dire que u/z imaginaire pure

=-u/z ?
Absolument
Ça donne des calculs bcp plus simples :lol3:
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 23 Jan 2011, 18:16
par tite_prune » 23 Jan 2011, 18:16
Ben alors on a u/z=i(10-z)/z
-u/z=-i(10-z)/z

=-i(10-z)/z donc c'est bon ça marche, est ce qu'il faut que je développe le z en z=x+iy?
Si j'ai pas besoin de développer en effet c'est 10000000 fois plus simple ^^

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 18:22
par Sa Majesté » 23 Jan 2011, 18:22
Non non il ne faut pas développer avec x+iy
Il faut juste remplacer u par i(10-z) dans l'égalité
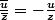
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 23 Jan 2011, 18:33
par tite_prune » 23 Jan 2011, 18:33
donc on a
}}{\bar z})
=-
}{z})
mais après je vois pas comment développer

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 18:35
par Sa Majesté » 23 Jan 2011, 18:35
Ben il faut simplifier : le conjugué d'un produit c'est le produit des conjugués
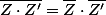
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 23 Jan 2011, 18:38
par tite_prune » 23 Jan 2011, 18:38
mais la on a un quotient non?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 18:40
par Sa Majesté » 23 Jan 2011, 18:40
i(10-z) j'appelle ça un produit :lol3:
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 23 Jan 2011, 18:47
par tite_prune » 23 Jan 2011, 18:47
a oui c'est vrai je suis bête !
Alors ça fait

=-
}{z})

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 18:50
par Sa Majesté » 23 Jan 2011, 18:50
Bon on a avancé d'un cran mais il ne faut pas s'arrêter là
Il faut simplifier : le conjugué d'une somme c'est la somme des conjugués
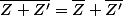
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 23 Jan 2011, 18:53
par tite_prune » 23 Jan 2011, 18:53
Donc je pense que ça marche aussi avec les soustractions =)
alors :
}{\bar z})
=-
}{z})

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 18:59
par Sa Majesté » 23 Jan 2011, 18:59
J'ai compris ta technique : c'est le pas à pas :ptdr:
Bon alors on va essayer de faire 2 pas maintenant
D'abord on peut simplifier par -i
Ensuite ça fait quoi
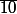
?
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 23 Jan 2011, 19:03
par tite_prune » 23 Jan 2011, 19:03
Oui parce que comm je voyais pas trop ce qu'il fallait faire jyvais doucement .
Donc
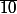
=10 et ensuite:

=


-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 19:05
par Sa Majesté » 23 Jan 2011, 19:05
Oui alors maintenant tu peux faire le produit en croix et simplifier
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 23 Jan 2011, 19:09
par tite_prune » 23 Jan 2011, 19:09
à la fin je trouve z=
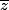
d'ou z-
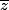
=0

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 19:12
par Sa Majesté » 23 Jan 2011, 19:12
tite_prune a écrit:à la fin je trouve z=
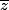
Oui et donc comment est z ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
