Exercices nombres complex
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 22 Jan 2011, 18:01
par tite_prune » 22 Jan 2011, 18:01
oui mais alors désolée je ne comprend pas ce qu'il faut faire. Pourriez-vous m'expliquer?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 22 Jan 2011, 18:04
par Sa Majesté » 22 Jan 2011, 18:04
Je te l'ai dit juste avant
Sa Majesté a écrit:Tu as à résoudre |u|=|z| donc |i(10-z)|=|z|
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 22 Jan 2011, 18:13
par tite_prune » 22 Jan 2011, 18:13
Donc après on a :
|i||10-z|=|z|

1|10-z|=|z|

|10|-|z|=|z|

|10|/2=|z|

|z|=5
Je sais pas si c'est juste mais je vois pas d'autre méthode pour résoudre ça.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 22 Jan 2011, 18:20
par Sa Majesté » 22 Jan 2011, 18:20
tite_prune a écrit:Donc après on a :
|i||10-z|=|z|

1|10-z|=|z|
Jusque là ça va
tite_prune a écrit:
|10|-|z|=|z|
Là c'est le drame :doh:
Tu n'as PAS |z'-z| = |z'|-|z|
A partir de |10-z| = |z|
tu peux utiliser la formule

-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 22 Jan 2011, 18:29
par tite_prune » 22 Jan 2011, 18:29
Formule que je n'ai pas dans mon cours mais le truc c'est que du coup je vois pas coment l'appliquer, parce qu'à la base on a pas de
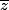
et là on peut en inclure un ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 22 Jan 2011, 18:35
par Sa Majesté » 22 Jan 2011, 18:35
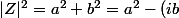^2 = (a+ib)(a-ib) = Z \cdot \bar{Z})
Comme tu as une équation entre nombres positifs
|10-z| = |z| est équivalent à |10-z|² = |z|²
soit
(10-\bar{z}) = z \bar{z})
Tu n'as plus qu'à développer et simplifier
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 22 Jan 2011, 18:38
par tite_prune » 22 Jan 2011, 18:38
d'accord donc j'ai à la fin:
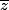
+z=1 est ce normal?
après je sais que
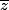
+ z = 2RE(z)

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 22 Jan 2011, 18:44
par Sa Majesté » 22 Jan 2011, 18:44
tite_prune a écrit:d'accord donc j'ai à la fin:
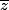
+z=1 est ce normal?
Pas 1 mais ...
tite_prune a écrit:après je sais que
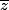
+ z = 2RE(z)
Oui il faut l'utiliser
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 22 Jan 2011, 18:50
par tite_prune » 22 Jan 2011, 18:50
Benalors j'ai refais mes calculs et je dois me tromper quelque part car je trouve 1.
Donc je développe :
100-10
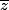
-10z+z
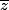
=z
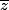
je simplifie par 10 et j'enlève les z
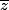
qui s'annulent donc : 1-
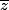
-z=0 et donc z+
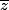
=1

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 22 Jan 2011, 18:51
par Sa Majesté » 22 Jan 2011, 18:51
Quand tu simplifies 100 par 10, qu'est-ce qu'il reste ? :ptdr:
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 22 Jan 2011, 18:52
par tite_prune » 22 Jan 2011, 18:52
Pardon ça doit etre la fatigue.. ( on va dire ça hein) oui donc j'ai z+
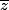
=10

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 22 Jan 2011, 18:54
par Sa Majesté » 22 Jan 2011, 18:54
Oui et donc ...
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 22 Jan 2011, 18:56
par tite_prune » 22 Jan 2011, 18:56
la partie réelle de z =5

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 22 Jan 2011, 18:58
par Sa Majesté » 22 Jan 2011, 18:58
Oui et donc ça fait quoi comme ensemble ?
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 22 Jan 2011, 19:07
par tite_prune » 22 Jan 2011, 19:07
L'ensemble T ( j'ai pas réussis a trouver la tex qui allait avec) qu'on à au début et dans ce cas MUDT est un parallélogramme!

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 22 Jan 2011, 19:11
par Sa Majesté » 22 Jan 2011, 19:11
Tu veux parler de l'ensemble

?
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 22 Jan 2011, 19:13
par tite_prune » 22 Jan 2011, 19:13
Sa Majesté a écrit:Tu veux parler de l'ensemble

?
oui mais en y réfléchissant ce n'est pas le même ici on à plutot l'ensemble: cercle de centre 0 et de rayon 5
oui non enfaite c'est même pas ça.. je desespère

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 22 Jan 2011, 19:16
par Sa Majesté » 22 Jan 2011, 19:16
Pourtant c'est pas compliqué
Quel est l'ensemble des points M du plan d'affixe z dont la partie réelle vaut 5 ?
Fais un dessin si tu ne vois pas
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 22 Jan 2011, 19:21
par tite_prune » 22 Jan 2011, 19:21
C'est la droite des points qui ont pour affixe 5?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 22 Jan 2011, 19:22
par Sa Majesté » 22 Jan 2011, 19:22
Je pense que tu as compris mais que c'est mal dit
Les points qui ont pour affixe 5, il n'y en a qu'un !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
