Volume boule grâce aux intégrales
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
thibaut47500
- Membre Naturel
- Messages: 70
- Enregistré le: 09 Fév 2010, 18:06
-
 par thibaut47500 » 30 Nov 2010, 20:51
par thibaut47500 » 30 Nov 2010, 20:51
Voila tout est dit dans le titre (ou presque) je dois retrouver le volume
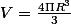
d'une boule grâce aux intégrales. J'ai compris que la boule est constituée d'une infinité de sphères ayant toutes un rayon différent mais après je bloque. Merci d'avance!
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Nov 2010, 21:00
par Nightmare » 30 Nov 2010, 21:00
Salut,
regarde [url="http://www.maths-forum.com/defi-d-intuition-volume-boule-dimension-quelconque-109804.php"]ce topic[/url]
-
thibaut47500
- Membre Naturel
- Messages: 70
- Enregistré le: 09 Fév 2010, 18:06
-
 par thibaut47500 » 30 Nov 2010, 21:07
par thibaut47500 » 30 Nov 2010, 21:07
J'ai pas tout compris donc voila j'aimerais trouver la formule qui permet de trouver toutes les surfaces des disques à partir de
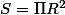
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Nov 2010, 21:09
par Nightmare » 30 Nov 2010, 21:09
C'est ce que je fais dans le 3ème post du topic vers lequel je t'ai orienté, il ne te reste plus qu'à le lire !
-
thibaut47500
- Membre Naturel
- Messages: 70
- Enregistré le: 09 Fév 2010, 18:06
-
 par thibaut47500 » 30 Nov 2010, 21:11
par thibaut47500 » 30 Nov 2010, 21:11
AH ok par contre quand tu dis que z=a et que a varie de -1 à 1 je peux remplacer ces deux valeurs numériques par des inconnues pour généraliser?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Nov 2010, 21:13
par Nightmare » 30 Nov 2010, 21:13
Oui bien entendu, je n'ai traité que le cas particulier d'une boule de rayon 1 ! Cela dit, une boule de rayon R est homothétique (de rapport R) à une boule de rayon 1, donc son volume est R^3 fois le volume de cette dernière.
-
thibaut47500
- Membre Naturel
- Messages: 70
- Enregistré le: 09 Fév 2010, 18:06
-
 par thibaut47500 » 30 Nov 2010, 21:15
par thibaut47500 » 30 Nov 2010, 21:15
Tu m'as l'air assez calé sur le sujet et tu me perds un peu. De plus je n'ai vu l'homothétie que depuis aujourd'hui. Voila j'en suis au point où je ne vois pas comment obtenir la racine que j'ai écrire précédemment.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Nov 2010, 21:24
par Nightmare » 30 Nov 2010, 21:24
Salut,
je ne comprends pas, de quelle "racine" parles-tu? Qu'est-ce que tu ne comprends pas dans ce que j'ai fait dans l'autre topic?
-
thibaut47500
- Membre Naturel
- Messages: 70
- Enregistré le: 09 Fév 2010, 18:06
-
 par thibaut47500 » 30 Nov 2010, 21:24
par thibaut47500 » 30 Nov 2010, 21:24
S'il vous plait c'est vraiment important que je comprenne cette parti.
-
thibaut47500
- Membre Naturel
- Messages: 70
- Enregistré le: 09 Fév 2010, 18:06
-
 par thibaut47500 » 30 Nov 2010, 21:25
par thibaut47500 » 30 Nov 2010, 21:25
Je ne comprends pas comment trouves tu le rayon des cercles.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Nov 2010, 21:32
par Nightmare » 30 Nov 2010, 21:32
Tu as fait un dessin? Tes disques sont centrés en (0,0,z) (sur l'axe des côtes) et inscrits dans la boule. Si j'appelle M le centre d'un des disque et P une de ces deux intersections avec la boule, le triangle OMP est rectangle en M et Pythagore fournit alors que MP²=OP²-OM²
MP c'est le rayon du disque, OP le rayon de la boule et OM la "hauteur" du disque dans la boule (= z)
-
thibaut47500
- Membre Naturel
- Messages: 70
- Enregistré le: 09 Fév 2010, 18:06
-
 par thibaut47500 » 30 Nov 2010, 21:37
par thibaut47500 » 30 Nov 2010, 21:37
Ah ok j'ai compris ^^ Donc la il me suffit de traduire ça sur la surface puis de faire l'intégrale allant de deux points que j'aurais nommé -R et R. Merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
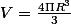 d'une boule grâce aux intégrales. J'ai compris que la boule est constituée d'une infinité de sphères ayant toutes un rayon différent mais après je bloque. Merci d'avance!
d'une boule grâce aux intégrales. J'ai compris que la boule est constituée d'une infinité de sphères ayant toutes un rayon différent mais après je bloque. Merci d'avance!