[MP] Sur les séries numériques
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 09 Nov 2010, 02:22
par euler21 » 09 Nov 2010, 02:22
Bonsoir
Je viens de travailler un DS de maths MP* qui traite des séries numériques. Le principe c'est qu'on considère une suite

à termes strictement positifs et que à partir de cette suite on définit d'autres. Notamment

qui est la moyenne géométriques des n premiers termes de la suite

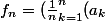^t)^{\frac{1}{t}})
et
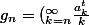^{\frac{1}{t}})
. Puis à partir de quelques chemins que je trouve complexes (introduction des suites auxiliaires, inégalités de Hölder ..) On arrive à prouver que les somme de ces suites sont majorées par la somme de

à un coefficient multiplicatif près dont on démontre qu'il est le plus petit possible. Notamment pour

ce coefficient est

, pour

c'est
^{-\frac{1}{t}})
, et pour
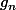
c'est
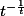
.
Ma question est ce que ce genre de démarches fait partie d'une branche spécifique des mathématiques?? Je pose cette question parce que je trouve cela vraiment très intéressant. (S'il existe des références ils seront les bienvenus)
Merci pour vos réponses
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Nov 2010, 12:37
par Nightmare » 09 Nov 2010, 12:37
Salut,
si tu parles du fait d'optimiser les bornes, on parle souvent justement d'optimisation, mais il n'existe pas vraiment de branche "optimisation" à proprement parlé en maths, ça fait parti de l'analyse plus globalement.
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 09 Nov 2010, 16:29
par euler21 » 09 Nov 2010, 16:29
Salut
Je ne sais pas si c'est correct, mais ce genre de résultats ne fait pas partie des théorèmes taubériens ??
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
