Polynome

[bisous1122]

Bonjour,

On me pose une équation
(m-2)x*+2(m-4)x+(m+4)(m+2)= 0 avec x l'inconnue

la question est
discuter, suivant les valeurs de m, l'existence et le nombre de solutions de cette équation


il y a t-il un lien avec les racines du polynome ?
si elles sont double ?

* x au carré

[Sa Majesté]

Salut

Oui il y a un lien :
Les racines du polynôme (m-2)x²+2(m-4)x+(m+4)(m+2) sont les solutions de l'équation (m-2)x²+2(m-4)x+(m+4)(m+2) = 0

[benekire2]

Salut,
Calcule le discriminant de ton équation , et étudie son signe :we:

[oscar]

Le discriminant simplifié est

(m-4)² - (m+4)(m²-4)=

Continue en distinguant les signes

Vérifie ton enoncé

[Dinozzo13]

Salut !
Soit l'équation de paramètre réel m :

1°) Que se passe-t-il si ?
2°)a) On considère . Calcule , le discriminant lié à cette équation.
b) Discute du signe de .

[Dinozzo13]

Si je ne me trompe pas, en ce qui concerne le signe de 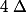, il n'existe qu'une valeur 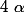pour laquelle 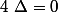telle que , tu pourras éventuellement démontrer cette conjecture grace au théôrème des valeurs intermédiaires en désignant la fonction définie sur 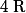par :
Par conséquent, 'y a pas 36 000 posibilités :ptdr: