bunny a écrit:Merci gigamesh d'avoir répondu.
2. a.
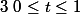
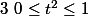
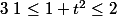
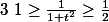

=> OK pour l'inégalité de gauche :

.
Ouaip, sauf que ta première équivalence n'en est pas une.
On a bien
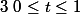
=>
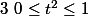
mais la réciproque n'est pas vraie.
Et la dernière équivalence n'est vraie que lorsque t est positif (ce qui est le cas ici, ceci dit).
bunny a écrit:Pour l'inégalité de droite, je n'ai pas bien suivi ton raisonnement.
Elle équivaut effectivement à

si l'on considère la proposition vraie. Or, on doit justement la prouver, c'est-à-dire utiliser un enchaînement d'inégalités comme tu me l'as astucieusement fais remarqué.
Peux-tu expliciter davantage ou est-ce une erreur de ma part ?
Ce qui te pose problème me semble-t-il, est l'aspect logique de la démonstration.
Lorsqu'on veut démontrer une proposition, on peut dire qu'elle est équivalent à une autre, qui est elle même équivalente à une troisième, etc, jusqu'à ce qu'on arrive par ce chaînage d'équivalence à une proposition dont on sait déterminer la véracité.
Mais écrire P Q R ne signifie pas qu'on affirme que P est vraie, ni qu'elle est fausse ; on affirme seulement que ces trois propositions P, Q et R sont toutes trois vraies ensemble ou bien toutes trois fausses ensemble.
p.ex, écrire ABC est rectangle en A BC²=AB²+AC² ne signifie pas qu'on affirme que ABC est rectangle en A; par contre on affirme que :
*si ABC est rectangle en A alors BC²=AB²+AC²
*si BC²=AB²+AC² alors ABC est rectangle en A
De même écrire (on suppose qu'on a A(2;3) et B(-1;5) dans un repère orthonormé)
M(x;y) est sur la médiatrice de [AB]
AM=BM
AM²=BM²
(x-2)²+(y-3)²=(x+1)²+(y-5)²
x²-4x+4 +y²-6y+9=x²+2x+1+y²-10y+25
-6x+4y-16=0
y=1,5x+4
ne signifie pas que M est sur la médiatrice de [AB], et n'affirme pas non plus que y est égal à 1,5x+4.
Cette chaîne d'équivalences signifie simplement qu'on a trouvé une CNS (une condition nécessaire et suffisante) pour qu'un point de coordonnées x et y soit sur la médiatrice de [AB].
Ainsi, la chaîne d'équivalences suivante prouve la deuxième inégalité :
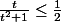
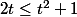
(on a multiplié par 2(t²+1) qui est strictement positif)
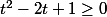
^2 \geq 0)
La dernière proposition est vraie (un carré est positif)
donc la première l'est aussi.
bunny a écrit:2. b.
Pour la démonstration par récurrence, je ne comprend toujours rien du tout. J'avais par contre déjà remarqué ce que tu as écrit. Mais en quoi cela nous avance-t-il ?
Il faut vraiment que quelqu'un m'aide pour la démonstration par récurrence. Je ne sais comment m'y prendre...
Merci de me répondre.
Bonne soirée.
On suppose que pour un certain entier k, on a
^k I_{2k+1}=ln(2))
On se propose d'en déduire que cette propriété est vraie au rang suivant k+1 ; ce qui signifie qu'on se propose de démontrer que
^{k+1} I_{2(k+1)+1}=ln(2))
Il suffit de prouver que
^{k+1} I_{2(k+1)+1}-ln(2)=0)
Et on se lance dans un calcul long et fastidieux, mais on sait où on va (on veut trouver zéro) et on sait ce qu'on va utiliser : l'hypothèse de récurrence, la définition de
)
et la propriété dont on a causé.
^{k+1} I_{2(k+1)+1}-ln(2)=u_k + \frac{(-1)^{(k+1)+1}}{k+1}-2(-1)^k I_{2k+3} -(u_k+2(-1)^kI_{2k+1})=....)
Bon courage !

