Bonjour
j'ai passé un contrôle où j'ai eu du mal, et la correction que j'ai obtenu n'est pas du tout assez détaillé. Donc si quelqu'un voudrait bien m'éclairer :
f(x) = e^(-x) ;)(8-2x^2 )
Il me faut la dérivée seconde de cette fonction
Merci beaucoup d'avance pour votre aide
Partiel L1 dérivée exponentiel
31 messages
- Page 1 sur 2 - 1, 2
par girdav » 20 Jan 2010, 10:03
Salut,
on calcule la dérivée première en utilisant la formule de dérivation d'un produit. Ensuite on dérive tout ça pour trouver la dérivée seconde.
Quel est ton résultat pour la dérivée première?
on calcule la dérivée première en utilisant la formule de dérivation d'un produit. Ensuite on dérive tout ça pour trouver la dérivée seconde.
Quel est ton résultat pour la dérivée première?
par Mathusalem » 20 Jan 2010, 10:08
Alors, poses
f(x) =
g(x) =
Et si tu as un produit de fonctions, tu dois faire
f(x)'g(x) + f(x)g(x)' = la dérivée de ton produit
f(x)' =
g(x)' =)
(-4x) <- derivée interne.
calcules f(x)'g(x) + f(x)g(x)', et redérives comme avant, sans oublier la dérivée interne.
f(x) =
g(x) =
Et si tu as un produit de fonctions, tu dois faire
f(x)'g(x) + f(x)g(x)' = la dérivée de ton produit
f(x)' =
g(x)' =
calcules f(x)'g(x) + f(x)g(x)', et redérives comme avant, sans oublier la dérivée interne.
par jaimelesmaths » 20 Jan 2010, 10:36
girdav, je sais bien quelle est la technique, mais j'ai pas réussi à l'appliquer dans ce cas précis la !
mathusalem, merci oui je connais cette formule, mais elle s'avère plus difficile lorsqu'il s'agit de la dérivée seconde, dans ce cas précis
pour la dérivée première j'ai trouvé, en reussissant à factoriser pour avoir un résultat plus soft :
(-e^(-x)) (8-2x²)^0.5 (1 + 2x (8-2x²)^-1)
j'ai eu ça dans la correction de mon prof, et ça va j'ai compris comment on en arrive à la. Cela dit pour la dérivée seconde il a mis un résultat mais je ne comprends pas quel formule il a utilisé.
Voici le résultat de la dérivée seconde. J'aimerais savoir comment on arrive à cela :
f"(x) = e^(-x) (8-2x²)^0.5 (1 + 2x (8-2x²)^-1) -
- e^(-x) (8-2x²)^0.5 [ 2(8-2x²)^-1 + 2x(4x(8-2x²)^-2)]
Voila je ne vois pas quelle formule il a utilisé. La premiere ligne de la dérivée seconde correspond à la dérivée premiere, puis il a soustrait à cela : je ne sais quoi !
Ca éclairerait ma journée si j'arrivais à bout de ce probleme !
mathusalem, merci oui je connais cette formule, mais elle s'avère plus difficile lorsqu'il s'agit de la dérivée seconde, dans ce cas précis
pour la dérivée première j'ai trouvé, en reussissant à factoriser pour avoir un résultat plus soft :
(-e^(-x)) (8-2x²)^0.5 (1 + 2x (8-2x²)^-1)
j'ai eu ça dans la correction de mon prof, et ça va j'ai compris comment on en arrive à la. Cela dit pour la dérivée seconde il a mis un résultat mais je ne comprends pas quel formule il a utilisé.
Voici le résultat de la dérivée seconde. J'aimerais savoir comment on arrive à cela :
f"(x) = e^(-x) (8-2x²)^0.5 (1 + 2x (8-2x²)^-1) -
- e^(-x) (8-2x²)^0.5 [ 2(8-2x²)^-1 + 2x(4x(8-2x²)^-2)]
Voila je ne vois pas quelle formule il a utilisé. La premiere ligne de la dérivée seconde correspond à la dérivée premiere, puis il a soustrait à cela : je ne sais quoi !
Ca éclairerait ma journée si j'arrivais à bout de ce probleme !
par jaimelesmaths » 20 Jan 2010, 10:41
girdav,
lorsque tu as dérivé ton g(x), tu as oublié un 2 au dénominateur, car :
(;)(u(x) ))^'= u'/(2;)u)
ps : comment faire un beau copier coller pour que les équations soit bien en forme mathématiques et non en ligne comme ceci?
lorsque tu as dérivé ton g(x), tu as oublié un 2 au dénominateur, car :
(;)(u(x) ))^'= u'/(2;)u)
ps : comment faire un beau copier coller pour que les équations soit bien en forme mathématiques et non en ligne comme ceci?
par Finrod » 20 Jan 2010, 10:42
Il a juste dériver la dérivé première.
en reprenant ta dérivé première, on a
=e^{-x}\\<br />g(x)=\sqrt{8-2x^{2}}\\<br />h(x)=\frac{2x}{\sqrt{8-2x^{2}}})
et = - v(x) (g(x)+h(x)))
qui se dérive en(g(x)+h(x)) - v(x) (g'(x)+h'(x)))
le truc qui te trouble est visiblement le h'+g' qui tu dois pourtant savoir calculer.
en reprenant ta dérivé première, on a
et
qui se dérive en
le truc qui te trouble est visiblement le h'+g' qui tu dois pourtant savoir calculer.
par Mathusalem » 20 Jan 2010, 10:46
Mathusalem a écrit:Alors, poses
f(x) =
g(x) =
Et si tu as un produit de fonctions, tu dois faire
f(x)'g(x) + f(x)g(x)' = la dérivée de ton produit
f(x)' =
g(x)' =
calcules f(x)'g(x) + f(x)g(x)', et redérives comme avant, sans oublier la dérivée interne.
=
voili voila
par jaimelesmaths » 20 Jan 2010, 10:51
oh c'est la dérivée de fonctions composées il me semble. Cela fait un moment que j'en avais pas fait effectivement ça m'étais sorti de la tête.
Je ne connaissais même pas cette formule en fait.
Ils nous foutent des trucs au contrôle qu'on a jamais vu en classe, c'est une aberration j'étais présente à tous les cours.
Thank youu so much ou plutôt danke schon tu es en allemagne !
Je ne connaissais même pas cette formule en fait.
Ils nous foutent des trucs au contrôle qu'on a jamais vu en classe, c'est une aberration j'étais présente à tous les cours.
Thank youu so much ou plutôt danke schon tu es en allemagne !
par Mathusalem » 20 Jan 2010, 10:57
Remarque : tu peux t'éviter les passages "difficiles" au niveau des règle de dérivées à savoir si tu développes le tout.. (Streng unempfohlen)
A+
A+
par jaimelesmaths » 20 Jan 2010, 10:58
mathu, je suis d'accord avec ta première ligne, mais tu peux détailler comment tu es passé à la seconde ligne s'il te plait?
par Finrod » 20 Jan 2010, 11:06
c'est "dankeshön"
si tu sépares, schon signifie déjà. D'ailleurs les Allemand adorent les mots bricolé avec d'autres. shön signifie beau et danke merci donc "dankeshön" est un beau merci.
Mes préférés c'est flugzug pour avion : flug : vole, zug: truc (donc truc qui vole)
et kuhlshrank pour frigo : kluhl: frais et schrank: placard (donc placard frais)
ps: mat réduit juste au même dénominateur en x par
le terme de gauche
si tu sépares, schon signifie déjà. D'ailleurs les Allemand adorent les mots bricolé avec d'autres. shön signifie beau et danke merci donc "dankeshön" est un beau merci.
Mes préférés c'est flugzug pour avion : flug : vole, zug: truc (donc truc qui vole)
et kuhlshrank pour frigo : kluhl: frais et schrank: placard (donc placard frais)
ps: mat réduit juste au même dénominateur en x par
par Mathusalem » 20 Jan 2010, 11:10
Exact, en général, quand t'as un produit de fonctions avec une qui est une racine, tu pourrais toujours t'arranger pour mettre au même dénominateur commun "joliment". En effet, j'ai une racine au dénominateur du côté droit et une racine au numérateur du côté gauche. En mettant au même dénominateur, j'ai donc la racine fois elle-même, et donc elle disparaît.
Je fais ça pour me ramener à une divison de fonction, dont la dérivée est à faire comme j'ai marqué auparavant.
A+
Je fais ça pour me ramener à une divison de fonction, dont la dérivée est à faire comme j'ai marqué auparavant.
A+
par SlowBrain » 20 Jan 2010, 11:11
Excuse-moi mais tu es dans quel L1? Si ta spécialité est les maths, alors les formules de base de dérivation sont supposées connues du lycée et il te faudra les rattraper. Tu ne viens pas de filière scientifique?
par jaimelesmaths » 20 Jan 2010, 11:19
je suis en L1 éco gestion. Je viens d'un bac ES. Je connais à priori toutes mes formules mais celle qu'a posté Finrod est super, c'est bien celle ci que mon prof a utilisé il me semble. Il y a beaucoup de maths en éco gestion donc oui j'ai interet a bosser les maths. Merci pour votre aide et vive l'allemand aussi.
par jaimelesmaths » 20 Jan 2010, 11:32
Finrod a écrit:Il a juste dériver la dérivé première.
en reprenant ta dérivé première, on a
et
qui se dérive en
le truc qui te trouble est visiblement le h'+g' qui tu dois pourtant savoir calculer.
Cela dit, Finrod, dans ton h(x) tu as oublié un "1+" devant. Donc est ce que ça fonctionne toujours si on le rajoute?
par jaimelesmaths » 20 Jan 2010, 17:17
wow j'avoue ne pas avoir accrocher. C'est poussé comme calcul, ça doit être très intéressant, si seulement je le comprenais.
par Finrod » 20 Jan 2010, 17:37
Arg !
Non j'ai pas oublié de 1 !
J'ai développé)
en
ps: j'ai appris l'allemand à l'arrache 2 moi avant de prendre mon poste en allemagne. Je peut parler mais Je ne comprend toujours rien à ce qu'ils disent. Fichu accent de vicking.
Non j'ai pas oublié de 1 !
J'ai développé
en
ps: j'ai appris l'allemand à l'arrache 2 moi avant de prendre mon poste en allemagne. Je peut parler mais Je ne comprend toujours rien à ce qu'ils disent. Fichu accent de vicking.
utiliser la structure du produit pour dériver
par mathelot » 21 Jan 2010, 12:23
bonjour,
je ne sais si ça simplifie, j'ai fait comme ça
dérivée logarithmique d'un produit de fonctions
de'=u'vw+uv'w+uvw')
on obtient
'}{uvw}=\frac{u'}{u}+\frac{v'}{v}+\frac{w'}{w})
le quotient
est la dérivée logarithmique
de la fonction u.
içi
=e^{-x} \sqrt{2} \sqrt{2+x} \sqrt{2-x})
(1)
en prenant les dérivées logarithmiques, il vient immédiatement:
)
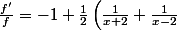en dérivant termes à termes une fois encore:
![](https://latex.ilemaths.net/ile_TEX.cgi?\displaystyle \frac{f"f-f'^2}{f^2}= - \frac{1}{2} \left( \frac{1}{(x+2)^2}+\frac{1}{(x-2)^2} \right))
en simplifiant
![](https://latex.ilemaths.net/ile_TEX.cgi?\displaystyle \frac{f"f-f'^2}{f^2}= - \frac{x^2+4}{(x^2-4)^2})
on multiplie par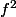
des deux côtés ce qui n'est pas vraiment un souci
![](https://latex.ilemaths.net/ile_TEX.cgi?\displaystyle f"f-f'^2= 2 \frac{x^2+4}{(x^2-4)} e^{-2x})
(2)
on reprend l'égalité (1) qu'on élève au carré
)
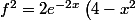dérivons une fois
)
)
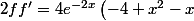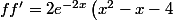dérivons encore une petite fois
![](https://latex.ilemaths.net/ile_TEX.cgi?\displaystyle f'^2+ff"= 2 e^{-2x} \left(-2x^2+4x+7))
(3)
en ajoutant (2) et (3) les
se simplifient:
![](https://latex.ilemaths.net/ile_TEX.cgi?\displaystyle f"f-f'^2= 2 \frac{x^2+4}{x^2-4} e^{-2x})
(2)
(3)
![](https://latex.ilemaths.net/ile_TEX.cgi?\displaystyle ff"= e^{-2x} \left( \frac{x^2+4}{x^2-4}- 2x^2 + 4x + 7 \right))
![](https://latex.ilemaths.net/ile_TEX.cgi?\displaystyle ff"= e^{-2x} \left( \frac{-2x^4+4x^3+16x^2-16x-24}{x^2-4}\right))
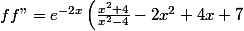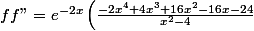reste à multiplier par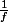
des deux côtés
![](https://latex.ilemaths.net/ile_TEX.cgi?\displaystyle f"= - e^{-x} \frac{1}{\sqrt{8-2x^2}} \left( \frac{-2x^4+4x^3+16x^2-16x-24}{4-x^2} \right))
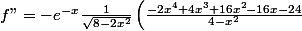![](https://latex.ilemaths.net/ile_TEX.cgi?\displaystyle f"(x) = e^{-x} \quad \frac{2x^4-4x^3-16x^2+16x+24}{\sqrt{2} (4-x^2)^{\frac{3}{2}}})
![](https://latex.ilemaths.net/ile_TEX.cgi?\displaystyle f"(x) = \sqrt{2} e^{-x} \quad \frac{x^4-2x^3-8x^2+8x+12}{ (4-x^2)^{\frac{3}{2}}})
c'est votre dernier mot ? oui,jean-pierre :we:
je ne sais si ça simplifie, j'ai fait comme ça
dérivée logarithmique d'un produit de fonctions
de
on obtient
le quotient
de la fonction u.
içi
en prenant les dérivées logarithmiques, il vient immédiatement:
en dérivant termes à termes une fois encore:
en simplifiant
on multiplie par
on reprend l'égalité (1) qu'on élève au carré
dérivons une fois
dérivons encore une petite fois
en ajoutant (2) et (3) les
reste à multiplier par
c'est votre dernier mot ? oui,jean-pierre :we:
31 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :