Partiel L1 dérivée exponentiel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jaimelesmaths
- Membre Naturel
- Messages: 24
- Enregistré le: 20 Jan 2010, 09:51
-
 par jaimelesmaths » 21 Jan 2010, 13:03
par jaimelesmaths » 21 Jan 2010, 13:03
Finrod a écrit:Arg !
Non j'ai pas oublié de 1 !
J'ai développé
)
en

ps: j'ai appris l'allemand à l'arrache 2 moi avant de prendre mon poste en allemagne. Je peut parler mais Je ne comprend toujours rien à ce qu'ils disent. Fichu accent de vicking.
excuse moi mais moi pour le développement que tu viens d'écrire, moi je trouve :
(8-2x²)^0.5 + (8-2x²)*(8-2x²)^-0.5
De plus, il y avait un 2x au numérateur, que tu as bien mis dans ton h(x), alors que la au numérateur tu as mis seulement 1
-
jaimelesmaths
- Membre Naturel
- Messages: 24
- Enregistré le: 20 Jan 2010, 09:51
-
 par jaimelesmaths » 21 Jan 2010, 13:11
par jaimelesmaths » 21 Jan 2010, 13:11
Plus précisement :
(8-2x²)^0.5 [1 + (8-2x²)^-1]
= (8-2x²)^0.5 + (8-2x²)^0.5 * (8-2x²)^-1
= (8-2x²)^0.5 + (8-2x²) * (8-2x²)^-0.5 (cette ligne est facultative)
Sachant qu'il y avait un 2x au numérateur car l'expression a la base c'était :
(-e^(-x)) (8-2x²)^0.5 [ 1 + 2x (8-2x)^-1 ]
-
jaimelesmaths
- Membre Naturel
- Messages: 24
- Enregistré le: 20 Jan 2010, 09:51
-
 par jaimelesmaths » 21 Jan 2010, 13:19
par jaimelesmaths » 21 Jan 2010, 13:19
en gros, moi pour le h(x) que tu avais posé, je pense que c'est :
h(x) = [ 2x * (8-2x²)^0.5 ] / (8-2x²)
-
jaimelesmaths
- Membre Naturel
- Messages: 24
- Enregistré le: 20 Jan 2010, 09:51
-
 par jaimelesmaths » 21 Jan 2010, 13:52
par jaimelesmaths » 21 Jan 2010, 13:52
mais bon je sais que c'est faux car ça rend la suite trop compliqué.
Je desespère.
-
mathelot
 par mathelot » 21 Jan 2010, 17:03
par mathelot » 21 Jan 2010, 17:03
-
jaimelesmaths
- Membre Naturel
- Messages: 24
- Enregistré le: 20 Jan 2010, 09:51
-
 par jaimelesmaths » 21 Jan 2010, 21:13
par jaimelesmaths » 21 Jan 2010, 21:13
excuse moi mathelot mais l'expression de base n'est pas celle ci. C'est :
f(x)=e^-x(8-2x²)^0.5
puis pour f'(x) on a :
f'(x) = (- e^-x) (8-2x²)^0.5 (1+2x(8-2x)^-1)
ce qui est plus compliqué c'est f"(x)
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 21 Jan 2010, 21:18
par Mathusalem » 21 Jan 2010, 21:18
C'est la même chose, mathelot a factorisé par deux sous la racine, puis en a extrait le 2.
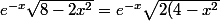} = e^{-x}\sqrt{2}\sqrt{4 - x^2})
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 21 Jan 2010, 21:23
par Finrod » 21 Jan 2010, 21:23
jaimelesmaths a écrit:Plus précisement :
(8-2x²)^0.5 [1 + (8-2x²)^-1]
= (8-2x²)^0.5 + (8-2x²)^0.5 * (8-2x²)^-1
= (8-2x²)^0.5 + (8-2x²) * (8-2x²)^-0.5 (cette ligne est facultative)
Sachant qu'il y avait un 2x au numérateur car l'expression a la base c'était :
(-e^(-x)) (8-2x²)^0.5 [ 1 + 2x (8-2x)^-1 ]
ouille c'est faux.
tu écris (8-2x²)^0.5 * (8-2x²)^-1 = (8-2x²) * (8-2x²)^-0.5 mais non. Si on écrit U=8-2x² ,
tu as écris :
U^{1/2}*U^{-1}=U*U^{-1/2} or en appliquant

on ne trouve pas cela.
Juste une confusion sur les puissances négatives.
le reste c'est ok, tu dois t'en sortir après.
-
mathelot
 par mathelot » 22 Jan 2010, 09:16
par mathelot » 22 Jan 2010, 09:16
................................................................... :help:
-
jaimelesmaths
- Membre Naturel
- Messages: 24
- Enregistré le: 20 Jan 2010, 09:51
-
 par jaimelesmaths » 22 Jan 2010, 20:08
par jaimelesmaths » 22 Jan 2010, 20:08
oui tu as raison finrod ! petit génie
-
jaimelesmaths
- Membre Naturel
- Messages: 24
- Enregistré le: 20 Jan 2010, 09:51
-
 par jaimelesmaths » 22 Jan 2010, 20:42
par jaimelesmaths » 22 Jan 2010, 20:42
enfin bref l'expression de base était (e^-x) (8-2x²)^0.5 (1 + 2x² (8-2x²)^-1)
c'est ce qu'il faut dériver.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
)

