Intégrales plan complexes et résidus
28 messages
- Page 1 sur 2 - 1, 2
intégrales plan complexes et résidus
Bonjour,
dans 2 jours j'ai mon examen, mais on nous a pas assez entrainé aux exercices et je n'arrive pas à trouver de méthode générale pour les résoudre...
on doit savoir calculer des intégrales par la méthode des résidus, ou simplement intégrer dans le plan complexe..
j'ai un exercice que je ne sais pas résoudre : l'intégrale fermée sur le cercle C de (sin(pi * z /4) )/ (z^2 - 1) dz où C est le cercle x^2 + y ^2 - 2x = 0 parcouru dans le sens direct.. il n'est pas indiqué d'utiliser la méthode des résidus mais le titre de l'exo est juste intégration dans le plan complexe..
peut etre savez vous comment résoudre cela?
ou l'intégrale de - pi à pi de (e^2ix) dx / (2 + cos x) à l'aide d'un changement de variable et de la méthode des résidus.. j'ai essayé de commencer, et pour cela en essayant de déterminer les pôles.. c'est évident qu'il faut rentrer dans les complexes puisque dans le plan réel, 2+ cos x ne peut etre égal à zéro!!
donc je me suis dit que je pouvais peut être écrire x sous la forme z = ro * e^(i * teta) avec ro = 2 et teta = (2k+1) pi tel que le cos soit égal à -1
mais je suis bloquée car si je mets x = z , dans ce cas j'ai le cos z et ça se simplifie pas comme je voudrais et ça ne fait pas -2!
merci d'avance!
dans 2 jours j'ai mon examen, mais on nous a pas assez entrainé aux exercices et je n'arrive pas à trouver de méthode générale pour les résoudre...
on doit savoir calculer des intégrales par la méthode des résidus, ou simplement intégrer dans le plan complexe..
j'ai un exercice que je ne sais pas résoudre : l'intégrale fermée sur le cercle C de (sin(pi * z /4) )/ (z^2 - 1) dz où C est le cercle x^2 + y ^2 - 2x = 0 parcouru dans le sens direct.. il n'est pas indiqué d'utiliser la méthode des résidus mais le titre de l'exo est juste intégration dans le plan complexe..
peut etre savez vous comment résoudre cela?
ou l'intégrale de - pi à pi de (e^2ix) dx / (2 + cos x) à l'aide d'un changement de variable et de la méthode des résidus.. j'ai essayé de commencer, et pour cela en essayant de déterminer les pôles.. c'est évident qu'il faut rentrer dans les complexes puisque dans le plan réel, 2+ cos x ne peut etre égal à zéro!!
donc je me suis dit que je pouvais peut être écrire x sous la forme z = ro * e^(i * teta) avec ro = 2 et teta = (2k+1) pi tel que le cos soit égal à -1
mais je suis bloquée car si je mets x = z , dans ce cas j'ai le cos z et ça se simplifie pas comme je voudrais et ça ne fait pas -2!
merci d'avance!
Merci beaucoup pour les réponses que vous m'apportez..
Bon alors comment je fais pour déterminer cette somme de résidus?
Cette notion d'indice de point ne me dit strictement rien..
Puis je utiliser P(zo)/Q'(zo) ?
Je ne sais vraiment pas comment commencer.. c'est ça mon problème pour tous les exercices
Bon alors comment je fais pour déterminer cette somme de résidus?
Cette notion d'indice de point ne me dit strictement rien..
Puis je utiliser P(zo)/Q'(zo) ?
Je ne sais vraiment pas comment commencer.. c'est ça mon problème pour tous les exercices
Ici, vu que la dérivée de Q(z)=z^2 - 1 n'est pas nulle au point z=1 (et z=-1), tu peut effectivement prendre la formule "toute cuite" P(zo)/Q'(zo).
Faire seulement gaffe que ca marche pas toujours (i.e. uniquement si Q'(zo) est non nul...)
Allez continue.
Si t'as pas vu les indices, c'est pas grave,
ça doit vouloir dire que, dans ton théorème des résiduts, tu doit intégrer sur un "contour de domaine parcouru dans le sens trigo".
Faut simplement faire attention que dans la "somme des résiduts", tu prend que ceux qui correspondent à des poles qui sont dans le domaine.
Par exemple, ici, des deux pôles 1 et -1, il n'y en a qu'un qui t'interesse.
Faire seulement gaffe que ca marche pas toujours (i.e. uniquement si Q'(zo) est non nul...)
Allez continue.
Si t'as pas vu les indices, c'est pas grave,
ça doit vouloir dire que, dans ton théorème des résiduts, tu doit intégrer sur un "contour de domaine parcouru dans le sens trigo".
Faut simplement faire attention que dans la "somme des résiduts", tu prend que ceux qui correspondent à des poles qui sont dans le domaine.
Par exemple, ici, des deux pôles 1 et -1, il n'y en a qu'un qui t'interesse.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Oui, car il n'y a qu'un seul des deux pôles à l'intérieur du disque dont le cercle est le bord (fait un DESSIN)new-physician a écrit:P/Q' pour 1 et - 1 = zo
au final j'obtiens : 2i pi * ( racine 2/2 + racine 2/6)
mais je ne tiens pas compte du contour donc c'est complètement faux !! =s
En plus, tu as du te gourrer dans un des deux résidus...
EDIT : en fait tu t'es gourré dans LES DEUX résidus...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Oui dans notre théorème des résidus, on a mis que le contour sur le domaine entoure les pôles dans le sens positif, donc ça doit correspondre au sens trigo!
Ah donc dans mon calcul précédent, il y a un pôle en trop.. mais lequel? Je ne sais pas comment le déterminer...
Donc mon prof a donné ces exos mais vu qu'on a pas traité les indices , on ne peut pas tenir compte de l'équation du cercle ou quoi? Je ne comprends pas trop!
Ou à moins qu'elle puisse me servir à déterminer le pôle inutile.. mais comment? intuitivement je dirais que c'est - 1 qui ne me sert pas.. on a affaire à un cercle de rayon racine de 2x et le rayon étant positif.. on ne peut avoir de z = - 1 non??
Ah donc dans mon calcul précédent, il y a un pôle en trop.. mais lequel? Je ne sais pas comment le déterminer...
Donc mon prof a donné ces exos mais vu qu'on a pas traité les indices , on ne peut pas tenir compte de l'équation du cercle ou quoi? Je ne comprends pas trop!
Ou à moins qu'elle puisse me servir à déterminer le pôle inutile.. mais comment? intuitivement je dirais que c'est - 1 qui ne me sert pas.. on a affaire à un cercle de rayon racine de 2x et le rayon étant positif.. on ne peut avoir de z = - 1 non??
Bon,
Le coup des indices, tu oublis complètement ...
J'ai posé cette question parce qu'il y a plusieurs façons d'énoncer le théorème des résiduts, dont une qui parle "d'indice" et je voulais savoir laquelle tu as.
Clairement, tu as la version "sans indices", qui permet de faire ce genre d'exercices sans problèmes.
Pour savoir quels sont les pôles qui servent, tu dois DESSINER le contour sur lequel tu intègre. L'énoncé précise que c'est un cercle et il faut que tu trouves le centre et le rayon.
Le rayon n'est surement pas 2x, c'est un "vrai nombre" (i.e. une constante)
Il faut rammener l'équation à quelque chose du genre (x-?)²+(y-?)²=?²
Le coup des indices, tu oublis complètement ...
J'ai posé cette question parce qu'il y a plusieurs façons d'énoncer le théorème des résiduts, dont une qui parle "d'indice" et je voulais savoir laquelle tu as.
Clairement, tu as la version "sans indices", qui permet de faire ce genre d'exercices sans problèmes.
Pour savoir quels sont les pôles qui servent, tu dois DESSINER le contour sur lequel tu intègre. L'énoncé précise que c'est un cercle et il faut que tu trouves le centre et le rayon.
Le rayon n'est surement pas 2x, c'est un "vrai nombre" (i.e. une constante)
Il faut rammener l'équation à quelque chose du genre (x-?)²+(y-?)²=?²
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
C'est la même méthode que pour les équation du secon degrés : il faut dire que "c'est le début d'une identité remarquable" :
x² + y² - 2x = 0
ssi (x²-2x+1) -1 + y² = 0
ssi (x-1)² + (y-0)² = 1²
C'est donc le cercle de centre (1,0) et de rayon r=1
Le point z=1 est bien dans le disque correspondant, mais le point z=-1 n'y est pas.
x² + y² - 2x = 0
ssi (x²-2x+1) -1 + y² = 0
ssi (x-1)² + (y-0)² = 1²
C'est donc le cercle de centre (1,0) et de rayon r=1
Le point z=1 est bien dans le disque correspondant, mais le point z=-1 n'y est pas.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bon, le deuxième exercice est trés nettement plus dur :
On te donne une intégrale réelle et il faut que tu la tripatouille pour en faire une intégrale complexe sur le bord d'un domaine.
Tu doit donc trouver :
1) le domaine que l'on va choisir.
2) la fonction que l'on va intégrer.
Il faut évidement savoir que la "passerelle" entre les deux types d'intégrales est :
\,{\rm d}z\ =\ \bigint_a^bf(\gamma(t))\,\gamma'(t)\,{\rm d}t)
où est une paramétrisation du bord
est une paramétrisation du bord  du domaine
du domaine  (dans le sens "direct")
(dans le sens "direct")
Ici, pour le domaine, comme il y a une intégrale de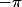 à
à  et des fonctions trigo. (le
et des fonctions trigo. (le 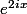 et le
et le ) ) il faut intuiter que le domaine c'est le disque centré en (0,0) de rayon 1 dont le bord est le cercle trigo.
) il faut intuiter que le domaine c'est le disque centré en (0,0) de rayon 1 dont le bord est le cercle trigo.
On prend donc la paramétrisation suivante du cercle trigo :

Il reste à trouver qui est la fonction f.
Ce n'est (quasi) jamais la fonction que l'on avait au départ sous le signe intégrale.
La formule générale nous dit que pour cette paramétrisation là, on a :
\,{\rm d}z\ =\ \bigint_{-\pi}^{\pi}f(e^{it})\,ie^{it}\,{\rm d}t\ \) (car
(car =ie^{it}) )
)
On cherche donc une fonction méromorphe telle que
telle que \,e^{it}\ =\ \frac{e^{2it}}{ 2+\cos(t) }) .
.
As tu une idée ?
On te donne une intégrale réelle et il faut que tu la tripatouille pour en faire une intégrale complexe sur le bord d'un domaine.
Tu doit donc trouver :
1) le domaine que l'on va choisir.
2) la fonction que l'on va intégrer.
Il faut évidement savoir que la "passerelle" entre les deux types d'intégrales est :
où
Ici, pour le domaine, comme il y a une intégrale de
On prend donc la paramétrisation suivante du cercle trigo :
Il reste à trouver qui est la fonction f.
Ce n'est (quasi) jamais la fonction que l'on avait au départ sous le signe intégrale.
La formule générale nous dit que pour cette paramétrisation là, on a :
On cherche donc une fonction méromorphe
As tu une idée ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Pourriez vous me définir méromorphe? est ce une fonction qui admet des pôles ou quoi?
Pour trouver cette fonction de z , ça me parait vraiment compliqué...
Je sais pas trop pour le dénominateur..
Pour le numérateur je dirais un truc du genre : -iz
donc ça me ferait f(z) = -iz / ( 2 + cos ..et c'est là que je ne sais pas ;) )
Pour trouver cette fonction de z , ça me parait vraiment compliqué...
Je sais pas trop pour le dénominateur..
Pour le numérateur je dirais un truc du genre : -iz
donc ça me ferait f(z) = -iz / ( 2 + cos ..et c'est là que je ne sais pas ;) )
28 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
