Classes d'équivalences
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Jan 2010, 16:24
par Nightmare » 15 Jan 2010, 16:24
Salut à tous !
Je considère dans

les n-uplets
_{i\le n})
qui sont rangés en ordre alterné, ie

(ou inversement)
Je considère que deux ensembles sont en relation lorsque ils ont les même inégalités. A savoir que
\sim (\beta_{i}))
si et ssi pour tout i et j, l'ordre entre

et

est le même que celui entre

et

.
On définit évidemment une relation d'équivalence. Combien il y a-t-il de classes d'équivalences (selon la valeur de n) ?
Exemple :
Les ensembles {3,7,5,9} et {4,7,6,15} sont en relation, mais {4,7,5,6} n'est pas en relation avec les deux derniers, puisque 7 > 6 alors que 7 < 9 et 7 < 15Je n'ai pas de réponses pour le moment (à part bien sûr les premiers cas n=1, 2..)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Jan 2010, 17:04
par Ben314 » 15 Jan 2010, 17:04
Salut,
Je suppose que ta question peut s'exprimer sous le forme :
"Parmi les n! classes dans N^n (presque) tout entier, combien sont dans ton fameux ensemble des 'alternées'" ?
Ce qui revient à chercher le nombre de permutations "alternées"...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Jan 2010, 17:11
par Ben314 » 15 Jan 2010, 17:11
Si on note

ce nombre, j'obtient :
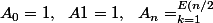}\left(\matrix{n-1\cr 2k-1}\right) A_{2k-1}\times A_{n-2k})
où
)
désigne la partie entière et
)
les coeff. binomiaux....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Jan 2010, 17:12
par Nightmare » 15 Jan 2010, 17:12
Salut Ben :happy3:
Qu'appelles-tu "mon ensemble des 'alternées' " ?
Je ne cherche pas à savoir combien j'ai d'ensemble que je peux ranger de manière alternées mais combien d'ensembles rangés de manière alternées sont rangés de la même manière (pour une manière et un entier n donnés)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Jan 2010, 17:20
par Ben314 » 15 Jan 2010, 17:20
Il y a n! (factorielle n) ordre possibles pour (x1,x2,...,xn) (en les supposant distincts), et, parmi ceux là, tu cherche lesquels vérifient x1x3 ; x3Ce n'est pas ça ta question ?
P.S. j'ai modifié mon précédent post qui contenait une erreur (j'avais oublié le coeff binomial...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Jan 2010, 17:29
par Ben314 » 15 Jan 2010, 17:29
Si tu veut une autre façon de voir, si
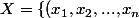\in{\bb N}^n {\rm\ tels\ que\ }x_i\not=x_j{\rm\ pour\ }i\not= j\})
alors

s'identifie naturellement avec le groupe alterné
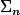
et, pour compter le nombre de classes de
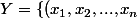\in{\bb N}^n {\rm\ tels\ que\ }x_1x_3,\ x_3x_5,\ ...\})
Il suffit de les compter dans
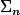
...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Jan 2010, 20:04
par Ben314 » 15 Jan 2010, 20:04
En tapant les 10 premières valeurs sous google, on tombe là dessus :
http://en.wikipedia.org/wiki/Alternating_permutationLes nombres en question sont des... Bernouillis...
Tient, tant que j'y suis, j'vais aussi faire "le prof" :
Nightmare a écrit:...Je considère que deux ensembles sont en relation...
C'est pas des ensembles mais des n-uplets...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Jan 2010, 14:41
par Nightmare » 16 Jan 2010, 14:41
Salut Ben !
Ok, j'ai compris maintenant qu'on parlait effectivement de la même chose. Le lien répond à la question, je te remercie :happy3:
PS : Sauf erreur, ils parlent d'ensembles aussi dans le lien :lol2:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Jan 2010, 15:20
par Ben314 » 16 Jan 2010, 15:20
Nightmare a écrit:PS : Sauf erreur, ils parlent d'ensembles aussi dans le lien :lol2:
C'est normal, les anglophones écrivent toujours n'importe quoi : ils n'ont pas lu Bourbaki :zen:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
