Systèmes de numération

[z33wolf]

Bonjour à tous.
Il y a un exercice que je n'arrive pas à résoudre et qui me trotte dans la tête depuis un petit temps déjà. Si quelqu'un pouvait m'aider à le résoudre, m'aiguiller ou quoi que ce soit, ce serait très sympa de sa part. =)
Voici l'intitulé :

Déterminer la base du système de numération dans laquelle 251 est un carré.

Merci d'avance.

[Ben314]

Salut,
Ton problème revient à chercher la base et 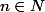tels que 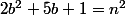c'est à dire (forme canonique) soit encore .
Cette équation diophantienne est assez complexe à résoudre...
Les premières solutions sont :
b=0, n=1 (exclu)
b=8, n=13
b=32, n=47
b=312, n=443
b=1128, n=1597
b=10640, n=15049
.
.
.

[z33wolf]

Merci beaucoup pour le coup de pouce ! =)
Cependant, si j'ai bien compris, plusieurs solutions sont possibles ? De plus, pourquoi b > ou égal à 6 obligatoirement ?

Sinon, pour des nombres dont le coefficient du b² était égal à 1, j'avais trouvé une autre méthode qui consistait en ceci :

Exemple avec 171.
b² + 7b + 1 = n²
(b + 1)² < n² < (b + 4)²
donc b + 1 < n < b + 4
d'où n = b + 2 OU n = b + 3
si n = b + 2 alors on a une solution impossible.
avec n = b + 3 on trouve b = 8 donc n = 11.
Reste ensuite à transformer pour avoir que :

[171]base8 = [13]²base8

et pour vérifier en base 10 :

[121]base10 = [11]²base10

Voilà.
Malheureusement, le problème est ici que j'ai affaire à du "2x²" ce qui m'empêche d'encadrer comme je l'ai fait dans mon exemple.

[Ben314]

Le vient tout simplement du fait que, comme le chiffre 5 apparait dans l'écriture de 251, la base doit au moins être égale à 6 (il n'y a pas de chiffre 5 dans la base 3 par exemple)
Effectivement, la méthode que tu propose marche trés bien pour des équations diophantiennes de la forme y²=x²+cst et c'est bien le cas dans l'exemple que tu donne.
Les équations y²=kx²+cst avec k>1 sont en général trés difficile à résoudre : la plus connue de toutes est l'équation de Pell-Fermat y²=kx²+1 dont les solutions sont données à l'aide de la fraction continuée de sqrt{k}...
Je ne sait pas si tu cherche toutes les solutions ou une seule (dans le deuxième cas, on peut en trouver en 'tatonant')

[z33wolf]

Merci beaucoup pour les précisions. =)
Normalement, je suis censé ne trouver qu'une solution (d'après l'énoncé), je ne savais même pas que plusieurs étaient possibles.
Dans ce cas-ci je vais garder la valeur la plus faible, la base étant donc 8 et le nombre recherché 15 (vu que le 13 trouvé est en base 10, il est à convertir en base 8, ce qui donne 15 si je ne m'abuse).
Encore merci. =)