Numération

par **minidiane** » 17 Sep 2009, 13:02

Bonjour je bloque complètement sur cet exercice:

On recherche un nombre N à trois chiffres.
En permutant, dans l'écriture de N, le chiffre des dizaines et celui des unités, on obtient l'écriture d'un nombre M.
En permutant, dans l'écriure de N, le chiffre des dizaines et celui des centaines, on obtient l'écriture d'un nombre P.
Les nombres M et P restent des nombres à tros chiffres.
Déterminer tous les nombres N qui vérifient simultanément les relations:
N+36=M et N-270=P.

Je bloque complètement j'ai beau chercher un système je tourne en rond.
J'ai vu que M-P=306, j'ai écris N=abc, M=acb et P=bac mais je ne vois pas comment faire.

par **girdav** » 17 Sep 2009, 13:06

;

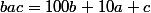
puis il faut écrire un système d'inconnues

et

.

par **minidiane** » 17 Sep 2009, 13:17

Je trouve:

9b-9c=-36
90a-90b=270

et j'ai aussi 90a-99b+9c=306

par **girdav** » 17 Sep 2009, 14:56

Je n'ai pas vérifié si ces équations sont correctes, mais tu peux simplifier par

toutes tes équations.

par **minidiane** » 17 Sep 2009, 15:06

Je trouve
b= c-36
a= c-39
Mais je n'arrive pas à en savoir plus.

par **girdav** » 17 Sep 2009, 15:16

Le système a, il me semble, un déterminant nul, donc il y a soit une infinité de solutions soit aucune. Je trouve avec ta première équation

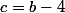
et la deuxième

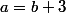
. Je crois qu'il y a des erreurs de simplification.

par **minidiane** » 17 Sep 2009, 15:25

En effet, je trouve la même chose maintenant.
Je trouve ainsi;
b= c-4
a= c-1
il y a sans doute une infinité de solutions vu l'énoncé, mais est-ce que ce système suffit pour répondre à la question?

par **girdav** » 17 Sep 2009, 15:34

Il y a encore des conditions sur

et

: ils doivent être entre

et

ce qui élimine des cas. Le plus dur et de l'écrire.

par **minidiane** » 17 Sep 2009, 15:42

donc on peut voir directement que c doit être supérieur à 4 sinon b est négatif, il sera donc supérieur à 1 pour que a soit positif lui aussi.
C'est le seul cas que je trouve pour l'instant

par **girdav** » 17 Sep 2009, 15:48

Donc regarde quand

;

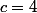
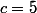
etc...

par **minidiane** » 17 Sep 2009, 16:04

ça marche pour chacun des c. Donc il faut que c soit compris entre 4 et 9.

par **girdav** » 17 Sep 2009, 16:07

Oui, il reste à écrire les solutions correspondant à chaque

.

par **minidiane** » 17 Sep 2009, 16:12

ok merci beaucoup de m'avoir aidé.
Voici ce que j'ai trouvé:
c=4->N=304, M=340 et P=034
c=5->N=415, M=451 et P=145
c=6->N=526, M=562 et P=256
c=7->N=637, M=673 et P=367
c=8->N=748, M=784 et P=478
c=9->N=859, M=895 et P=589

par **girdav** » 17 Sep 2009, 16:16

Ca doit être ça!

Numération

Numération

Qui est en ligne