Numération
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Jan 2007, 15:16
par sue » 24 Jan 2007, 15:16
bonjour
je cherche à déterminer a, b, x t.q :
})^2 = \overline{bbb}^{(x)})
.
ben on a
^2 = b(x^2+x+1))
, mais j'ai juste traduit l'énoncé je sais pas comment faire aprés .
merci pour votre aide :we:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 24 Jan 2007, 15:27
par fahr451 » 24 Jan 2007, 15:27
on développe à gauche on fait la division euclidienne de a^2 par x
a^2 = qx +c
en regardant les termes en x^3 on se rend compte que q = 0; les termes constants donnent c = b
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Jan 2007, 15:30
par sue » 24 Jan 2007, 15:30
ok merci Fahr451 pour la réponse , je regarderai surement ce soir mnt je dois partir pour mon entrainement :we:
merci
-
andros06
- Membre Relatif
- Messages: 180
- Enregistré le: 30 Aoû 2006, 13:30
-
 par andros06 » 24 Jan 2007, 15:31
par andros06 » 24 Jan 2007, 15:31
Bon déjà je suis d'accord avec ta traduction d'énoncé.
Si tu résous l'équation en x, tu vas obtenir deux racines. Apres tu dois arriver à formuler des conditions sur a et b sachant que la (les) racine(s) doivent être entière, que le dénominateur doit diviser le numérateur, qu'un nombre sous la racine doit être positif etc ... apres faut faire le tri .
Ya ptetre plus simple et plus rapide mais de cette façon tu dois pouvoir y arriver ...
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Jan 2007, 19:53
par sue » 24 Jan 2007, 19:53
bonsoir Fahr451
désolée je comprend pas trés bien :triste: , comment puis-je donc trouver c ?
s'agit-il d'une égalité polynomiale ou une équation ? parce que qd vous me dites q=0 , je comprend qu'il s'agit juste d'identifier les termes des deux polynomes .
pouvez-vous m'expliquer un peu plus svp ? je suis un peu perdue :briques:
merci
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 24 Jan 2007, 19:56
par fahr451 » 24 Jan 2007, 19:56
ah non ce n'est pas une égalité entre polynômes
la décomposition en base x est unique
a1a2a3( le tout barre) = b1b2b3 ( le tout barre) ssi pour tout i ai = bi
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Jan 2007, 20:03
par sue » 24 Jan 2007, 20:03
ok , je comprends pourquoi q=0 , sinon comment je détermine c ?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 24 Jan 2007, 20:10
par fahr451 » 24 Jan 2007, 20:10
regarde les termes "constants" ( unités) des deux membres.
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Jan 2007, 20:30
par sue » 24 Jan 2007, 20:30
oui je vois bien q=0 et b=c , mais encore comment je détermine c ? :triste:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 24 Jan 2007, 20:37
par fahr451 » 24 Jan 2007, 20:37
il reste les termes en x à regarder
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Jan 2007, 20:39
par sue » 24 Jan 2007, 20:39
b=0 ? :briques:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 24 Jan 2007, 20:40
par fahr451 » 24 Jan 2007, 20:40
je trouve la même chose...
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Jan 2007, 20:45
par sue » 24 Jan 2007, 20:45
ça me semble bizarre moi ..donc a=0 i.e pour tt x entier !!!
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 24 Jan 2007, 20:45
par fahr451 » 24 Jan 2007, 20:45
ça m'intrigue aussi quelque peu
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Jan 2007, 20:59
par sue » 24 Jan 2007, 20:59
on a x > 1 , pourtant ici c'est valable pour tt x entier naturel ...
je crois que le cas d'entiers nuls est évident peut-on supposer qu'ils sont non nuls ? si déjà on peut trouver de tels entiers !
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 24 Jan 2007, 21:08
par fahr451 » 24 Jan 2007, 21:08
honnètement je ne vois pas la faille dans ce que j'ai dit, et pourtant on aurait pu s'attendre à une solution non triviale sinon pourquoi poser un tel exo.
fais moi signe
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Jan 2007, 22:03
par sue » 24 Jan 2007, 22:03
ok , fahr451 je te remercie déjà pour tt (si vous me permettez de vous tutoyer biensur :we: )
sinon pourquoi poser un tel exo.
fais moi signe
ben j'en sais rien moi , c'est un exo comme tt les exo posés dans le livre .
en tt cas il me semble qu'il n'y a pas de solutions non trivial (ce n'est que de l'intuition), j'essaye de le montrer en supposant que les entiers sont non nuls et x > 1 .
donc si on réecrit l'égalité donnée sous la forme :
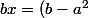(x+1))
que peut-on dire de l'existence de tels entiers naturels ??
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 24 Jan 2007, 22:05
par fahr451 » 24 Jan 2007, 22:05
sue je l 'ai démontré . la seule chose c'est que ce résultat m 'intrigue
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Jan 2007, 22:15
par sue » 24 Jan 2007, 22:15
sue je l 'ai démontré
comment ? est-ce le fait de trouver une solution triviale élimine la possibilité de trouver une autre solution meme si on a posé d'autres conditions : entiers naturels non nuls ?
désolée je te fatigue par mes questions

:triste:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 24 Jan 2007, 22:24
par fahr451 » 24 Jan 2007, 22:24
je reprends tout
a^2(x+1)^2 = a^2 x^2 + 2a^2 x + a^2 = bx^2 +bx +b
si dans a^2 il y a une "retenue" c'est à dire si a^2 >=x
le nombre de droite a un chiffre des "milliers" (coef de x^3 ) non nul
or le nombre de droite n 'en a pas donc
a^2 < x donc ce sont les deux mêmes écritures en base x et on a :
a^2 = b (en regardant le chiffre des "unités")
puis bx^2 + 2b x = bx^2 +bx d'où b = 0
la seule solution est 0
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités